`Free Top-Surface' case

  

Figure: Plots of the limiting interface amplitude, $(n_1)_\mathit{max}$(--), and the associated free surface amplitude, $(n_2)_\mathit{max}$ ($-\;-\;-$), for $0.04\le \rho _2/\rho _1\le 0.99$ in steps of 0.05. Note the higher curves on the left (for both $(n_1)_\mathit{max}$ and $(n_2)_\mathit{max}$ pertain to the lower $\rho _2/\rho _1$ ratios.

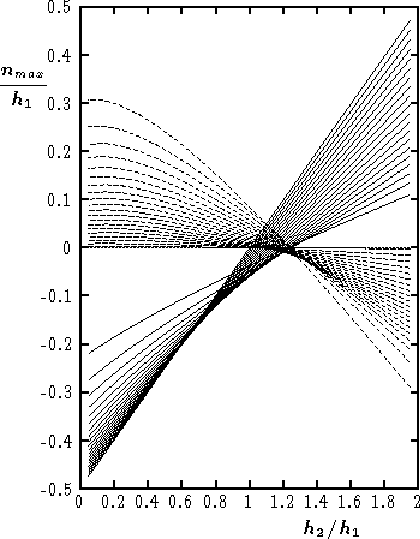
The conjugate flow conditions given above can be solved numerically for free-surface boundary conditions as done by Evans (1996). In this case, there does not appear to be nice analytic forms¹, analagous to (6) and (7). It is imperative therefore to represent the numerical solutions for the amplitudes graphically as shown in Figure 3, where the limiting surface and pycnocline amplitudes, n₁ and n₂, are plotted for $0.04\le \rho_2/\rho_1\le .99$ in steps of 0.05 over a range of h₂/h₁ values between 0 and 2.

Note that at the larger oceanic ratios of $\rho_2/\rho_1\lesssim 1$ the pycnocline limiting amplitudes, $(n_1)_\mathit{max}$, are largest and the free-surface limiting amplitudes, $(n_2)_\mathit{max}$, are smallest. In fact when $\rho _2 \sim \rho _1$, $n_1 \rightarrow (h_2-h_1)/2$, and then asymptotes to the `rigid-lid' limiting amplitude. Note also that free-surface and pycnocline amplitudes are always of opposite sign and thereby become zero simultaneously at situations pertaining to congruent conjugate flows as described by the free-surface locus in Fig. 4. Hence, negative interfacial amplitude internal waves appear to have an associated free top surface `bulge' whilst positive interfacial amplitudes are accompanied by a free top surface `depression'.

Figure 4 shows the locus of the situations, characterised by values of $\rho _2/\rho _1$ and h₂/h₁, at which the conjugate flows become `congruent' (i.e. $h_2^\prime = h_2$, $h_1^\prime = h_1$ and $c_1^\prime=c_2^\prime=c$), implying the limiting amplitudes, n₁ and n₂, are zero. Of course this marks the boundary between positive and negative internal waves.

  

Figure: The boundaries between negative (to the left) and positive (to the right) internal wave solutions, as determined by congruent conjugate flows. The solid (--) line (after Evans (1996)) pertains to the free-surface boundary condition whilst ($-\;-\;-$) represents the analytic boundary, $\rho _2/\rho _1= (h_2/h_1)^2$, that pertains to the ``rigid-lid'' boundary condition, as follows from (6).

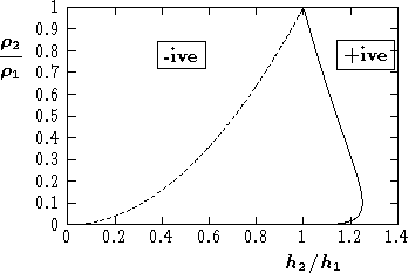Remarkably, it is observed that the locus of congruent conjugate flows for the ``free-surface'' case is confined entirely to the range $h_2/h_1 \ge 1$ and appears to end as well as start at values of h₂/h₁ = 1. Thus it appears that, with free surface boundary conditions, no positive internal waves are possible at any density ratio if $h_2\le h_1$. The maximum value of h₂/h₁ on the locus is 1.25and occurs when $\rho_2/\rho_1= 0.1$. These numbers are certainly valid to high numerical accuracy and, probably, can be shown to be exact.

At this point, it is apposite to sound a note of caution. In the limit when $\rho_2/\rho_1\rightarrow 0$ and $h_2\gg h_1$, it might be supposed that the motion of the bottom layer is unaffected by the presence of the tenuous upper layer and should behave like a normal ``1-layer'' solitary wave. The conjugate flow limiting amplitude in this situation would appear from (6) to be $(n_1)_\mathit{max} \sim h_2$ i.e. as large as we care to make h<sub>2</sub>. Of course, this conclusion does not accord with what we know of the maximum solitary wave that has a $120^\circ$ Stokes corner and a limiting amplitude of $0.83319918\,h_1$(Evans and Ford 1996a; Williams 1981). Both of these `extremal scenarios', though different, are ``exact'' insofar as the relevant integral equations are exactly satisfied.

This heralds the question of stability. In our opinion it is most likely that the ``conjugate flow'' picture of an extremal form of infinite width will prove unstable especially at the lower values of $\rho _2/\rho _1$ - indeed it is not clear that it is stable for any density ratio. Though a formidable task, this underlines the need for a stability analysis of all large amplitude internal wave solutions.

Acknowledgements:

The author is grateful for discussions on these topics with Prof. L. Vázquez, Dr. W.G. Easson, Dr. I-Fan Shen and Prof. G.L. Alfimov. This work was partially supported by a British Council ``Acciones Integradas'' award (ref: MDR/(1996/97)/1828) and the NATO grant (ref: OUTR.LG-960298).