 |
 |
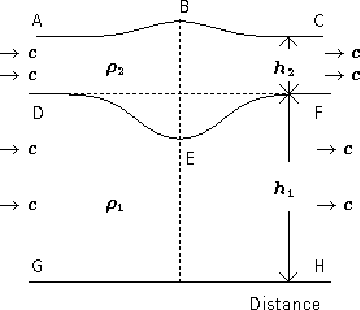
Oceanic internal waves arise principally because the density of the
ocean water is not constant. To a fair approximation we may think of an
upper, warmer layer of density, ![]() ,
and undisturbed depth
h2, above a deeper, colder and more saline layer of density
,
and undisturbed depth
h2, above a deeper, colder and more saline layer of density
![]() and depth, h1, as depicted in
Fig. 1. These layers meet at the ``thermocline'' or
``pycnocline'' which is normally marked by a sharp change in water
temperature with depth. Internal waves have amplitudes that distort the
thermocline and the surface profile, though, in oceanic situations the
latter deformation is much smaller and often ignored in theories that
assume a ``rigid-lid'' (i.e. flat top surface) boundary condition.
In the deeper marginal seas where internal waves are observed, h1 is
normally much larger than h2. This implies negative amplitude
at the thermocline and, consequently, negative total
mass (Evans and Ford 1996a).
and depth, h1, as depicted in
Fig. 1. These layers meet at the ``thermocline'' or
``pycnocline'' which is normally marked by a sharp change in water
temperature with depth. Internal waves have amplitudes that distort the
thermocline and the surface profile, though, in oceanic situations the
latter deformation is much smaller and often ignored in theories that
assume a ``rigid-lid'' (i.e. flat top surface) boundary condition.
In the deeper marginal seas where internal waves are observed, h1 is
normally much larger than h2. This implies negative amplitude
at the thermocline and, consequently, negative total
mass (Evans and Ford 1996a).
Though not as destructive as ``tsunamis'', the larger oceanic
internal waves carry a considerable amount of energy and the associated
current flows can be strong enough to be an important factor in the
design of coastal oil platforms and similar sea structures. Hence it is
important to estimate the ``worst scenario'' i.e. the question of
``how large![]() ?'' can various properties be is of paramount
importance. This puts the emphasis on estimating the size and associated
currents, vorticity etc. of the maximal internal wave in any given
oceanic locality. Of course, this presupposes the maximal internal wave
form can be generated by the prevailing, natural formation forces. This
is by no means clear and, hence, there is also the allied need to
understand the mechanism(s) of formation of oceanic internal waves. Some
time ago, Osborne and Burch 1980; Osborne 1990 observed very large internal waves in the
tropical Andaman sea. These were prevailingly easterly moving and
tended to recur after the semi-diurnal period of 12 hrs 26 mins which
indicates convincingly that tidal forces play a key part in their
formation mechanism. Unlike normal tides, there is no evidence of any
correlation between internal wave size and the phases of the Moon. If,
indeed, the formative forces are primarily tidal in origin, then the
waves should be highly predictable with virtually no randomness. This
would suggest that the extremal wave is limited by the magnitude
of the prevailing tidal forces rather than by the maximal stable
internal wave solution corresponding to the parameters at that location.
?'' can various properties be is of paramount
importance. This puts the emphasis on estimating the size and associated
currents, vorticity etc. of the maximal internal wave in any given
oceanic locality. Of course, this presupposes the maximal internal wave
form can be generated by the prevailing, natural formation forces. This
is by no means clear and, hence, there is also the allied need to
understand the mechanism(s) of formation of oceanic internal waves. Some
time ago, Osborne and Burch 1980; Osborne 1990 observed very large internal waves in the
tropical Andaman sea. These were prevailingly easterly moving and
tended to recur after the semi-diurnal period of 12 hrs 26 mins which
indicates convincingly that tidal forces play a key part in their
formation mechanism. Unlike normal tides, there is no evidence of any
correlation between internal wave size and the phases of the Moon. If,
indeed, the formative forces are primarily tidal in origin, then the
waves should be highly predictable with virtually no randomness. This
would suggest that the extremal wave is limited by the magnitude
of the prevailing tidal forces rather than by the maximal stable
internal wave solution corresponding to the parameters at that location.
However, the latter is certainly an upper bound on the extremal form at any given location and is also, mathematically, a well-defined problem. Accordingly much attention has been devoted to this task. The nature of the solutions sought invalidate the small amplitude/long wavelength conditions required for an accurate description via the KdV theory. Consequently, integral equation techniques whose numerical solutions should be exact within potential flow have
 |
been utilised in order to gain insight on these extremal forms.
Assuming rigid-lid boundary conditions, Turner and Vandenbroeck (1988) computed
extremal forms of internal waves for parameters,
h2/h1= 1,
![]() (which are decidedly not typically oceanic)
and concluded that the limiting form was one of finite amplitude and
very large width - the middle part being essentially predictable as a
uniform ``2-layer-flow'' domain that is ``conjugate'' to the
outskirts flow where the fluid flow velocities in both layers is c.
Evans and Ford (1996b) utilised a different integral equation form to
investigate the limiting internal wave with oceanic parameters,
h2/h1=1/3 and
(which are decidedly not typically oceanic)
and concluded that the limiting form was one of finite amplitude and
very large width - the middle part being essentially predictable as a
uniform ``2-layer-flow'' domain that is ``conjugate'' to the
outskirts flow where the fluid flow velocities in both layers is c.
Evans and Ford (1996b) utilised a different integral equation form to
investigate the limiting internal wave with oceanic parameters,
h2/h1=1/3 and
![]() .
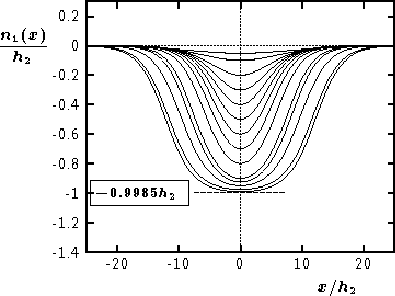
Their results are shown in
Figure 2. Again it was seen that, at the largest amplitudes,
the `width' appears to diverge and, moreover, the largest solution
amplitude,
.
Their results are shown in
Figure 2. Again it was seen that, at the largest amplitudes,
the `width' appears to diverge and, moreover, the largest solution
amplitude,
![]() ,
agreed precisely with the predicted
value from ``conjugate flow'' considerations viz.
-0.9985h2 (shown as
a horizontal dotted line in the figure).
,
agreed precisely with the predicted
value from ``conjugate flow'' considerations viz.
-0.9985h2 (shown as
a horizontal dotted line in the figure).