|

|

|

|

|

|

|
| Back to WHOI Arctic Group Projects | ||||||||||||||||||||||||||||||||||||||||
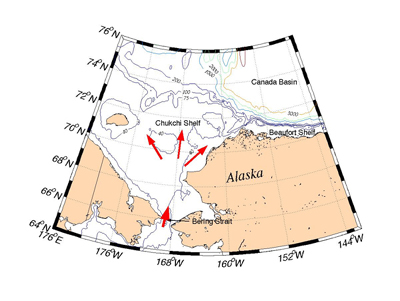
Directly beneath the ice cover of the deep Arctic basins is a 50-100
m layer of relatively fresh water that is near the freezing temperature.
This surface layer is separated from the underlying warmer, saltier
Atlantic water by the cold halocline layer, in which the temperature
is near freezing while the salinity increases rapidly with depth.
The cold halocline water is not a simple mixture of the surface layer
and the Atlantic water. Aagaard et al. (1981) suggested that the cold
halocline layer must be maintained by the lateral injection of cold,
salty water; the most likely source being from the broad, shallow
Arctic continental shelves where cooling rapidly reduces the temperature
to near freezing and salt rejection accompanying ice formation can
increase the salinity (and, hence, density) of the shelf waters.
Numerical modeling studies can be grouped into two broad categories:
(1) full-physics simulations, and (2) process studies. Full-physics
simulations attempt to use a comprehensive model with complete physics,
the most realistic geometry, forcing and boundary conditions either
to reproduce existing observations or to predict future behavior.
In our view, it is often difficult to isolate and understand individual
processes that are embedded among many processes in such models. Frequently,
the "numerical data" must be analyzed in the same manner as real ocean
observations, making the interpretation unclear.
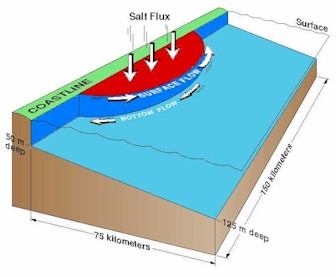
We began with the simplest coastal polynya scenario we could imagine
-- a static polynya of specified size and shape with an imposed salt
flux at the surface to mimic the primary effect of salt rejection
accompanying ice formation (Figure
2). The coastline is assumed straight and the bottom slopes gently
away from the coast. We ignore the details of wind forcing and ice
dynamics, and assume a constant ice formation rate (i.e. constant
surface buoyancy flux). Figure
2: Schematic of the geometry of our idealized, static polynya.
A surface salt (or density) flux is applied within the half-elliptical
region adjacent to the straight coastline (colored red). Initially
the density of water beneath the salt flux increases. Geostrophic
currents develop along the edge of the polynya, as indicated
by the arrows. Eventually, this rim current develops instabilities
that grow into eddies and move away from the polynya, carrying
the denser water with them (Figure
3). [Larger image]
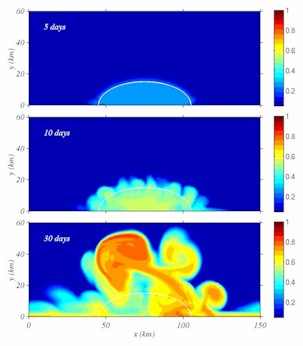
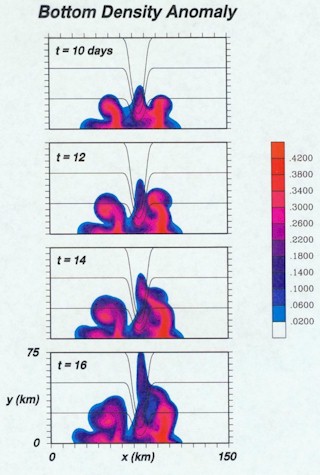
Figure
3: Plan views of the density increase at the bottom at three
different times for an idealized, static polynya. A constant surface
density flux is imposed within the white half-ellipse adjacent to the
coastline. The colorbar indicates the density increse in kg/m^3. [Larger image]
We have examined some effects of bottom topography and ambient alongshelf
currents on the formation and offshore transport of dense water from
coastal polynyas. First, we included a single submarine canyon that
intersected the original idealized, static polynya (Chapman and Gawarkiewicz,
1995). The basic formation of dense water eddies was qualitatively
identical to the smooth topography cases. However, eddies that happen
to move into the canyon quickly cascade down the steep canyon walls
and are channeled offshore as an intermittent gravity current that
rides along the right wall of the canyon into deeper water (Figure
5). The gravity current tends to "pulse" as each eddy passes.
The current is slow and strongly stratified, so little mixing with
ambient fluid takes place, in marked contrast to gravity currents
associated with large overflows, e.g. the Mediterranean Sea. The model
features are consistent with recent observations of dense water currents
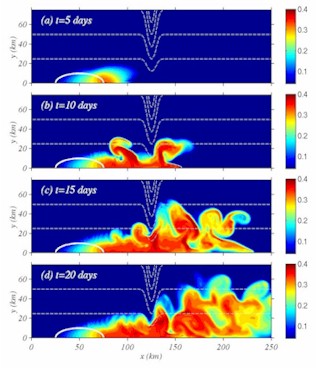
in Barrow Canyon (Weingartner et al., 1998). Figure
5: Plan views of the density anomaly at the bottom at four
different times for an idealized, static polynya with a constant
surface density flux (as in Figure
3), but with a submarine canyon intersecting the polynya
(indicated by the black depth contours). As eddies move close
to the canyon, they slide down the steep canyon walls and flow
along the canyon axis as a slow and intermittent gravity current.
The colorbar shows the density increase in kg/m^3. [Larger image]
| ||||||||||||||||||||||||||||||||||||||||
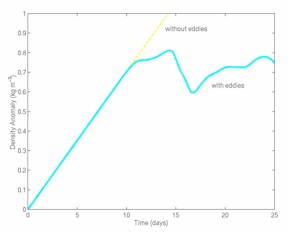
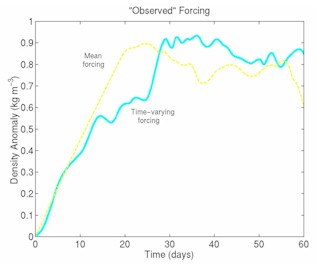
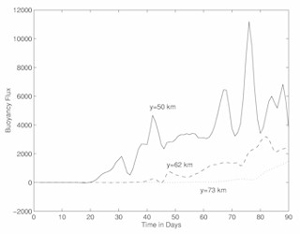
The static polynya studies assume that the polynya remains open with a fixed shape and that the ice formation rate is constant. Of course, real polynyas open and close on time scales of days to weeks, with their shapes varying tremendously. In fact, polynyas may not remain open long enough for the quasi-equilibrium to be reached. To address these issues, an investigation of the ocean response to time-dependent polynyas has been made (Chapman, 1999). The opening and closing of the polynya was modeled using the Pease (1987) model in which polynya width is determined by a balance between the surface wind stress blowing the newly formed ice offshore (opening the polynya) and the new ice formation (closing the polynya). Using idealized atmospheric variables (air tempreature and wind speed), as well as estimates based on observations, it was shown that the ocean basically integrates the effects of short-duration polynyas and behaves in much the same manner as the idealized, static polynyas. The density within the polynya increases with each successive polynya until eddies form and begin to carry the dense water away from the polynya region. The density increase is then limited, despite additional polynya events throughout the winter. The time-dependent response is nearly the same as if the polynya were static and forced with the seasonally averaged surface buoyancy flux, suggesting that the simple algebraic estimates of density increase may be useful even for variable polynyas on longer time scales (Figure 7). The effect of dense water transport across an idealized continental
shelf has important implications for exchange between the shallow continental
shelves and the deep ocean basins within the Arctic Ocean. Gawarkiewicz
(2000) found that dense water eddies are capable of inducing flows which
cross the shelfbreak. Using ambient (linear) stratification which is
typical of the Chukchi Shelf, and forcing typical of coastal polynyas,
the dense water was injected over the continental slope at a depth of
100 m, roughly the depth of the shelfbreak (Figure
8). A theoretical estimate of this depth of maximal transport of
dense water was developed, which depended on both the strength of the
surface buoyancy forcing in the coastal polynya as well as the strength
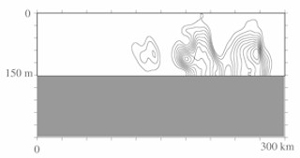
of the ambient stratification. Figure
8 : Along-slope distribution of a passive tracer seaward of
the shelfbreak after 90 days of a model run. The maximum concentrations
are at a depth of 90 to 120 meters, which is similar to the depth
of the shelfbreak. The tracer was initialized next to the coast,
within an idealized coastal polynya. [Larger image]
Several estimates have been made of the total amount of dense water
capable of feeding the cold halocline layer that could be produced
on Arctic continental shelves by coastal polynya processes (e.g. Cavalieri
and Martin, 1994; Winsor and Bjork, 2000). These results are based
on estimates of salt rejected during ice formation, which is then
available to increase the density of the shelf water. However, the
studies have not included a dynamical ocean model to determine the
actual density increase from the polynyas. Therefore, Winsor and Chapman
(2001) have used the polynya model of Winsor and Bjork (2000) to force
an idealized ocean model to estimate the dense water production on
the Chukchi Shelf for the winters of 1978-1998. | ||||||||||||||||||||||||||||||||||||||||
|
Aagaard, K., L. K. Coachman, and E. Carmack, 1981. On the halocline of the Arctic Ocean. Deep-Sea Res., 28A, 529-545. Cavalieri, D.J. and S. Martin, 1994. The contributions of Alaskan, Siberian, and Canadian coastal polynyas to the cold halocline layer of the Arctic Ocean, J. Geophys. Res., 99, 18343-18362. Chapman, D.C., 1997. A note on isolated convection in a rotating, two-layer fluid, J. Fluid Mech., 348, 319-325. Chapman, D.C., 1998. Setting the scales of the ocean response to isolated convection, J. Phys. Oceanogr., 28, 606-620. Chapman, D.C., 1999. Dense water formation beneath a time-dependent coastal polynya, J. Phys. Oceanogr., 29, 807-820. Chapman, D.C., 2000. The influence of an alongshelf current on the formation and offshore transport of dense water from a coastal polynya, J. Geophys. Res., 105, 24007-24019. Chapman, D.C. and G. Gawarkiewicz, 1995. Offshore transport of dense shelf water in the presence of a submarine canyon, J. Geophys. Res., 100, 13373-13387. Chapman, D.C. and G. Gawarkiewicz, 1997. Shallow convection and buoyancy equilibration in an idealized coastal polynya, J. Phys. Oceanogr., 27, 555-566. Gawarkiewicz, G. and D.C. Chapman, 1995. A numerical study of dense water formation and transport on a shallow, sloping continental shelf. J. Geophys. Res., 100, 4489-4507. Gawarkiewicz, G., 2000. Effects of ambient stratification and shelfbreak topography on offshore transport of dense water on continental shelves, J. Geophys. Res., 105, 3307-3324. Narimousa, S., 1996. Penetrative turbulent convection into a rotating two-layer fluid, J. Fluid Mech., 321, 299-313. Pease, C. H., 1987. The size of wind-driven coastal polynyas, J. Geophys. Res., 92, 7049-7059. Spall, M.A. and D.C. Chapman, 1998. On the efficiency of baroclinic eddy heat transport across narrow fronts, J. Phys. Oceanogr., 28, 2275-2287. Visbeck, M., J. Marshall and H. Jones, 1996. Dynamics of isolated convective regions in the ocean, J. Phys. Oceanogr., 26, 1721-1734. Weingartner, T.J., D.J. Cavalieri, K. Aagaard and Y. Sasaki, 1998. Circulation, dense water formation, and outflow on the northeast Chukchi Shelf. J. Geophys. Res., 103, 7647-7661. Winsor, P. and G. Bjork, 2000. Polynya activity in the Arctic Ocean from 1958 to 1997, J. Geophys. Res., 105, 8789-8803. Winsor, P. and D.C. Chapman, 2001. Distribution and interannual variability of dense water production from coastal polynyas on the Chukchi Shelf, J. Geophys. Res., submitted.
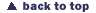
|