Abstract. Recently shallow water solitons have become a major topic of interest to both oceanographers and ocean acousticians. Numerous research efforts are underway to identify and predict soliton properties that are unique to each scientific discipline. In this work preliminary results are presented from a cross-disciplinary study of shallow-water solitons that utilizes oceanographic models, ocean acoustic models, oceanographic data, and ocean acoustic data. It is concluded that all four entities are required to fully understand and predict the impact that shallow-water solitons have on ocean-acoustic signal transmission.
 

Introduction

The stimulation for our study was initiated by the observation of an anomalous frequency response in shallow-water sound propagation measurements. In particular, acoustical measurements in the Yellow Sea conducted by Zhou, Zhang and Rogers[1] showed an anomalous drop in acoustical intensity, of about 30 dB, at a range of 28 km for acoustic frequencies around 630 Hz. The measured transmission loss was found to be time and direction dependent. The authors performed transmission loss calculations using an acoustic parabolic equation (PE) model and a gated sine function representation of solitons in the thermocline. The simulation results from this hypothetical case showed that an anomalous transmission loss can occur around 630 Hz when acoustical waves and solitons interact. Computer simulations subsequently confirmed [2,3] that the resonant like transmission loss is caused by an acoustical mode coupling due to the presence of solitons, together with a corresponding larger bottom attenuation for the coupled acoustic modes. At the "resonant" frequency (~630 Hz) acoustic modes are coupled and energy is passed from one mode to another. When the acoustic mode receiving the energy has a higher bottom attenuation than the other acoustic mode, a net loss in transmitted energy occurs. Over a long distance these losses become additive and can result in a large transmission loss. The entire process resembles a resonance phenomenon.[2,3]

Since the Zhou, et al. studies, the acoustical and oceanographic properties of bores and solitons have been studied in many areas. Surveys have been performed on the New Jersey and New England continental shelves. During the summer of 1995 SWARM[4] (shallow-water acoustics in a random medium ) was conducted on the continental shelf region off the New Jersey coast. The Shelfbreak PRIMER[5] experiment addresses an integrated acoustic and oceanographic field study in the middle Atlantic bight. Other acoustic predictability experiments where solitons are present have been performed.

We are presently performing studies of solitons and their anomalous effects on the intensity of the acoustical field in the Yellow Sea and the Strait of Messina regions. The Yellow Sea is a shallow sea, with a maximum depth of around 80 meters in the center. The semidiurnal tides are very strong and reach magnitudes of around 2 m/sec along sections of the Korean and Chinese coasts. Our work is concentrated to the south of the Shan-Tung peninsula in an area where the acoustical transmission loss measurements of Zhou, et al.[1] were conducted. There the water depth varies from 40 to 50 meters. ERS-1 satellite SAR images suggest that solitons are present in the area. The generation mechanism of solitons in this region is under investigation at present. The objective is to provide both oceanographic and acoustic model simulations that can corroborate the assumptions and findings of Zhou, et al. No oceanographic data were taken by Zhou, et al., thus, their assumption that solitons were the cause of the anomalous loss seen in their data remains unsupported.

In contrast to the Yellow Sea, the Strait of Messina is a narrow channel that separates the Tyrrhennian and Ionian Seas. It contains a sill that raises to within 80 meters of the surface. The semidiurnal tidal amplitudes at the northern and southern boundaries of the strait are only 17 and 10 cm respectively. There is, however, a large phase difference, of 174 degrees. The large phase difference and the geometrical constraints result in tidal velocities that can reach 3 m/sec. The motion of the semidiurnal tide over the sill depresses the thermocline and generates a bore. As the tide reverses a hydrologic jump of the bore occurs to the other side of the sill. The bore propagates away from the sill and its leading edge disintegrates into solitons, through amplitude and frequency dispersion.
 

Resonance occurrence and mechanisms

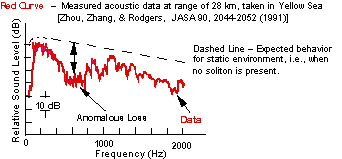
Zhou, et al.[1] have measured the frequency response of sound propagation in an area of the Yellow Sea that is located south of the Shan-Tung peninsula. The data was collected at various times over a period of four years. The source and receiver were located below the strong summer thermocline. Their measured power spectra at a range of 28 km have been published[1] and is reproduced here as Fig. 1. Their data shows an anomalous drop in acoustical intensity at around 630 Hz.
 
 
 

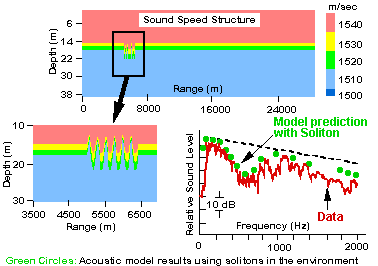
Corresponding transmission loss calculations, with no representation of solitons, using the acoustic parabolic equation (PE) model do not show an anomalous drop in acoustical intensity at 630 Hz. When, however, a hypothetical gated sine function representation of a soliton train is postulated in the thermocline, the PE model calculation shows a drop of acoustical intensity at around 630 Hz in agreement with the data. This good agreement between data and model prediction was first published by Zhou, et al [1] and is reproduced in Fig. 2.
 
 
 

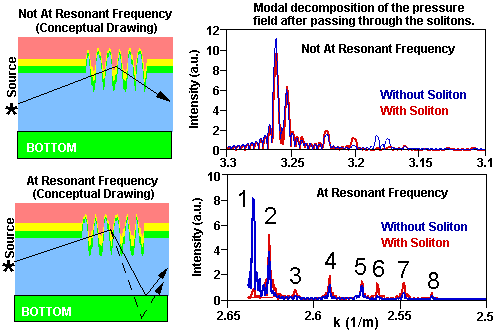
The physical mechanism for the resonant lose of acoustical intensity at a particular frequency can be understood in terms of mode coupling and energy redistribution among the normal (propagating) modes. Acoustical intensity calculations for the normal modes show that for frequencies outside of the narrow bandwidth containing the resonant frequency, a redistribution of energy does not occur when the solitons are present. This is shown in Fig. 3 (upper right) where the simulated acoustic pressure field has been decomposed into its spectral (wavenumber) components. The mode intensities are virtually unchanged when the soliton is placed between the source and receiver. However, near and at the resonant frequency, the redistribution of energy among the modes is quite different when the soliton is present between source and receiver (Fig. 3, lower right). The presence of the soliton results in acoustic mode coupling, redistributing energy from the lowest-order mode (mode 1) into higher-order modes (modes 2, 3, 4, 5, 6, and 7). The simulation modeling results shown in Fig. 3 are our duplication of the acoustic modeling analysis done by Zhou, et al.[1]. We have used high-fidelity PE models, FEPE and RAM[6,7] in the simulations shown in Fig. 3. The new FEPE and RAM PE models use improved energy conservation techniques[8]; their predictions represent both an improvement on, and verification of the results published by Zhou, et al.[1].
 
 
 

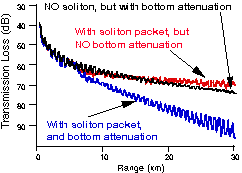
Mode coupling and the associated redistribution of energy among the modes will not result in the large loss in transmitted signal seen in Fig. 1 unless the higher-order modes have a significantly greater bottom attenuation than do the lower order mode(s). This was the situation shown in Fig. 1 where the higher-order modes (2 through 8) had a bottom attenuation that was an order of magnitude larger than the lower-order mode (mode 1). This cumulative loss over the 28 km track resulted in the large loss shown in Fig 1 for frequencies around 630 kHz.

The important role that the ocean bottom has in the soliton resonance effect is shown in Fig 4 where Yellow Sea acoustic simulations were made[3] for the following three cases: (1) soliton present but bottom attenuation was set to zero; (2) no soliton was present but bottom attenuation was present; and, (3) both soliton and bottom attenuation were present. The soliton redistributes the sound speed of the media; at the resonance frequency this produces mode coupling and a redistribution of energy among the propagating modes. However, when no bottom attenuation is present (or if each mode has identical attenuation), the total pressure due to the redistributed modes is the same as it was before the redistribution. In fact, Fig. 4 shows that the affect of bottom attenuation is more significant on signal loss than is the presence of solitons. The greatest loss occurs when both solitons and higher bottom attenuation (in the higher-order modes) are present.

In summary, at the resonant frequency the acoustic field interacts with the soliton packet and acoustic mode coupling occurs; this results in mode conversions (acoustic energy is redistributed from lower-order to higher-order modes). When the converted modes have higher bottom attenuation than the original modes, high signal loss can occur at the resonance frequency. If the bottom attenuation is not significantly higher for the converted modes, then only a modest signal loss will occur. If the acoustic frequency is not at or near the resonance frequency, no appreciable loss will occur due to the acoustic field passing through the soliton. It should be noted that the mode coupling and mode conversions can go from lower-order modes to higher-order modes and vice-versa. Furthermore, these mode conversions occur continually as the acoustic field passes through the environmental inhomogeneity (i.e., soliton) and that the environmental inhomogeneity is in a media where random fluctuations are continuously occurring. Thus, the problem is a very complex and difficult one.
 
 
 

It has been asserted that the simple relationship between the soliton's spatial wavenumber (K_Soliton) and the adjacent wavenumbers (k_{Acoustic modes}) of the propagating acoustic modes can predict the frequency (or wavelength) where mode coupling is likely to occur[1].

We have used computer simulations to show that it is the "effective" horizontal (or vertical) component of K_Soliton in Eq. (1) that is important. This is shown in Fig. 5(a) where the track between source and receiver is parallel (O=0) to the propagation direction of the soliton, and at angles, O, to the propagation direction of the soliton. Note that the "effective" horizontal (or vertical) component of K_Soliton in Fig. 5(a) will change as O changes, i.e., as the source-receiver track changes relative to the soliton's direction of propagation.

Figure 5(b) shows a computer simulation for a soliton environment similar to that used in the Yellow Sea simulations. Note that significant signal loss occurs at two resonant frequencies for transverse angles O=0 and O=50°, and does not occur at all for O=30°. Note also that while large signal loss is observed for both O=0 and O=50°, the magnitude of the losses and the resonant frequencies are different in the two cases. These results are consistent with Eq. (1) and the concept of "effective" horizontal (or vertical) component of K_Soliton .
 
 

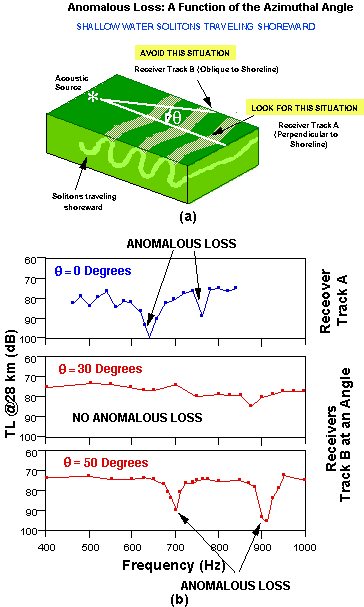
Soliton Modeling in the Strait of Messina and the Yellow Sea.

In the Strait of Messina, we are performing simulations of solitons with a two-layer reduced gravity model. The model was developed at the University of Hamburg by Brand, et al.[9]. It is formulated in terms of equations for the transport and variation of layer thickness. The channel width enters into the transport formalism besides the layer thickness and velocity. The topography is in the lower layer and the interface deviation is able to intersect it. Density is prescribed in each layer. The model is essentially two dimensional with grid points in the horizontal and layers in the vertical. Its formalism is weakly non-hydrostatic.

Solitons are generated in the sill region by the semidiurnal tide. The varying tide depresses the thermocline and generates bores that propagate away from the sill.Under favorable conditions the nonlinear terms cause the leading edge of the bore to steepen. Then through amplitude and frequency dispersion the boredisintegrates into solitons. The parameters of the model are the prescribed densities, the depth of the thermocline (top layer thickness), depth of ocean, topographic variations, and semidiurnal tidal amplitudes and phase.

We have performed a parameter space study of conditions representing summer, fall, and winter. We have conducted simulations of physical states encountered during the October 1995 cruise in the Strait of Messina that was conducted by NATO's SACLANT Undersea Research Center in La Spezia, Italy. Sensitivity studies of parameter ranges were also undertaken.
 
 
 

Case #	hl			Tides	Topo	Width
8	30m	1026.5	1028.0	M	M	M
8a	15m	1026.5	1028.0	M	M	M
8b	60m	1026.5	1028.0	M	M	M
8t	30m	1026.5	1028.0	M	Tyr-150m	M
9	30m	1026.5	1028.5	M	M	M
10	30m	1026.5	1029.0	M	M	M
10a	30m	1027.0	1028.0	M	M	M
10b	30m	1027.5	1028.0	M	M	M
11	50m	1028.2	1029.0	M	M	M
11a	50m	1028.5	1029.0	M	M	M
11b	150m	1028.5	1029.0	M	M	M
11q	50m	1028.5	1029.0	M	Tyr-150m	M
11v	50m	1028.5	1029.0	M	Ion-200m	M
11t	30m	1026.5	1028.0	Ai=30cm/s	M	M

The most relevant case studies and corresponding parameter values are listed in Table 1. The point of departure for the simulations was a range of parameter values encompassing summer values and conditions encountered during the October 1995 cruise in the Strait of Messina. Case 8 reflects a summer situation.

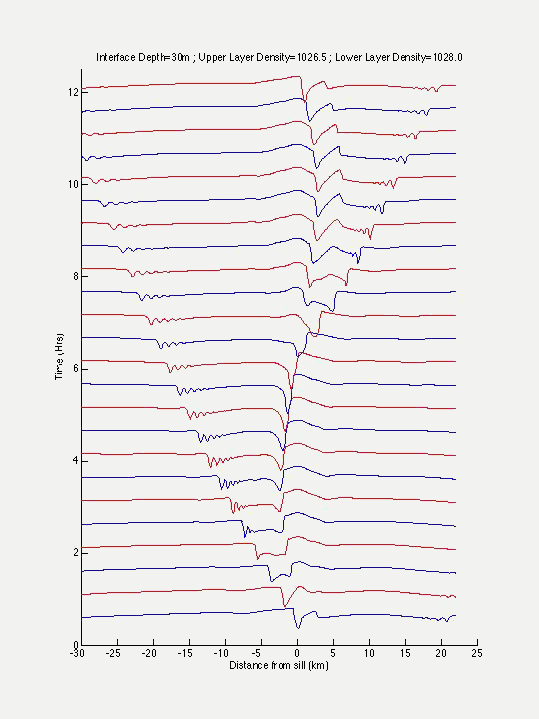
We have plotted a progression diagram of the interface deviation for case 8 in Fig. 6. The semidiurnal tide moves over the sill, depresses the thermocline, and generates a bore. As the tide reverses the bore retreats and does a hydrologic jump over the sill. Its leading edge propagates away from the sill and steepens through the action of the nonlinear terms. As it propagates amplitude and frequency dispersion set it and it disintegrates into solitons. The wavelengths of the solitons increase in time through the action of the nonlinear terms. The amplitudes decrease in the process and are damped by the viscous terms.

Cases 9 and 10 represent larger stratifications with increasing density values in the lower layer.

We analyzed the phase speed, C, of the solitons. For a two-layer model, it can be expressed as,

where  is the change in density, h₁ is the distance from the sea surface to the thermocline, h₂ is the distance from the thermocline to the sea floor, and g is the acceleration due to gravity.

As the stratification is increased, cases 8, 9, and 10 in Table 1, the phase speed of the solitons increases as expected. The amplitude of the solitons does not change among the three cases. The number of solitons on the south side of the strait remains the same. On the north side cases 9 and 10 have two more solitons than case 8. The topography on the north side is shallower than on the south side. The channel width on the north side is larger. The nonlinear dynamics must be influenced by the geometrical constrains.

In the set of cases 8, 10a, and 10b the stratification is decreased. From 8 to 10a and 10b, the phase speed of the solitons decreases. The solitons of case 10b have a larger amplitude than those of case 8. Case 10b, however, has fewer solitons on the north and south side of the sill in relation to case 8. This is counter to expectations since as the amplitude increases more solitons tend to appear.

A winter type of situation is represented in case 11b. The phase speed in this case is influenced by the decreased stratification and the increased upper layer depth. The solitons have a larger amplitude then in case 8. They appear, however, only on the south side of the sill. No solitons are generated on the north side. The topography on the north side of the sill is shallow and ranges from 400 to 600 m. The upper layer depth of 150 m is becoming comparable in magnitude to the lower layer depth. As a result the nonlinear effects in the upper layer tend to be compensated by the nonlinear terms of the lower layer, resulting in less steepening of the bore's edge and no disintegration into solitons.

In case 8t we have restricted the topography on the north side of the sill, Tyrrhennian Sea, to 150 m. This results in no solitons on the north side but more of them appear on the south side relative to case 8. The phase speed on the south side is somewhat smaller than in case 8.

In the Yellow Sea we are using a 2.5-D level nonhydrostatic model. The model is based on the Navier Stokes approach with prognostic equations for the velocities (u,v,w) and temperature and salinity. It is 2.5-D because the derivatives along the y-axis are neglected, Martin[10]. The Coriolis force is included. The boundaries are rigid at the top and bottom with prescribed inflow and outflow. Viscosity is included.

The physical parameters of the model are the stratification (temperature and salinity), depth of thermocline and halocline, topographic variations, depth of the ocean, Coriolis effects, and tidal amplitude/phase.

South of the Shan-Tung peninsula the semidiurnal tide can have velocities from 40 to 80 cm/sec along the coast, Guo-hong[11]. We used the value of 1 m/sec for forcing the model at the left boundary. The topography in the area of concern is in the 40 to 50 m range. The prescribed topographic variation was a step type idealized drop over 8 km down to 50 m from a 20 m coastal shelf.

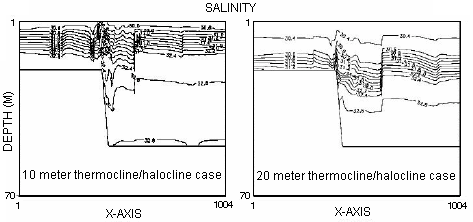
For our initial simulations we have prescribed summer conditions. Generic temperature and salinity profiles were constructed on the basis of monthly climatology and measurements by Lie[12] in August of 1983. Some of the results for a thermocline/halocline location of 10 and 20 meters are shown in Fig. 7. At 20 hours the second train of solitons is propagating away from the shelf. The remains of the first soliton train are still visible as a depression of the thermocline near the right hand side boundary. The depression of the thermocline eventually recovers to the original position in time and space. This space behavior can be seen proceeding left from the remains of the first soliton train. The spatial recovery is characteristic of the semidiurnal tidal influence on the thermocline. The damping of the first soliton train is brought about by model viscosity. The initial over the step depression leads, also, to a bore like disturbance that propagates on to the shelf.

The first soliton train has advanced closer to the right hand boundary for the 20 m thermocline as compared to the 10 m one. The 20 m thermocline has a larger effective upper layer depth and therefore a higher soliton phase velocity, as discussed before for the Strait of Messina.
 
 
 

A zoom of the third soliton train at 32 hours is shown in Fig. 8. The 10m thermocline case has about 4 solitons in the train. The initial thermocline depression is around 8 m. The wavelength of the first soliton in the train is around 200 m. The horizontal resolution of the model is 100 m and therefore coarse for resolving the solitons in the train. Vertical resolution is 1 m.
 
 
 

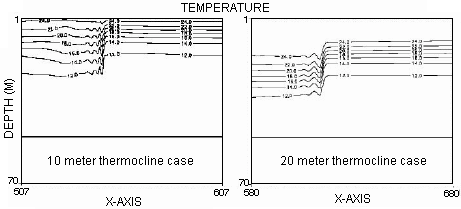
The 20 m thermocline solitons train is shown on the right hand side of Fig. 8. The initial depression is the same as before, 8 m. The wavelength of the first soliton is around 400 m. This solitons train has moved faster, traveled further and undergone more spreading through the nonlinear effects.
 

Concluding remarks.

We are studying a drop in acoustical intensity that can occur in shallow water around the resonant frequency. The phenomena has been shown to occur when solitons are present. The mechanism for the anomalous intensity drop in presence of solitons consists of energy transfer to higher acoustical modes. The intensity of the modal energy is attenuated by bottom effects.

Our studies are conducted in the Strait of Messina and the Yellow Sea. We are approaching the problem from the experimental, modeling, and theoretical side. In the Yellow Sea we have measurements that show an anomalous drop in acoustical intensity at around 630 Hz. We have shown that the resonant drop is due to solitons by performing transmission lose calculations with a parabolic equation (PE) model and a postulated soliton train. Model results show a drop around 630 Hz, in agreement with data.

We are presently modeling the solitons in the Yellow Sea with a nonhydrostatic level model. Our preliminary results indicate generation and propagation of solitons in an area south of the Shan-Tung peninsula. The simulated solitons will be coupled with acoustical PE models in the future.

In the Strait of Messina we have performed a parameter space study of soliton generation and propagation. The parameters span the summer to winter seasons and the conditions of the October 1995 cruise that tracked the solitons with a CTD chain. The phase speed trends are sensitive to upper layer thickness and density differences between the layers. This reflects the pycnocline shape or its strength and location in depth. On the seasonal scale the model's upper layer convergence behavior agrees with the trends of SAR data.

A 2-D sound speed was extracted from the two-layer model simulations. The approach is based on a perturbation expansion of the transport equation for the sound in conjunction with the two-layer model. It is analogous to the expansion for the density in conjunction with two-layer modeling that was used in Essen's Ph.D. thesis[13], at the University of Hamburg. The result gives the sound speed as a mean state versus depth plus a perturbation consisting of the vertical derivative of the sound speed times the interface deviation from the two layer model. The mean state of the sound speed can come from climatology or measurements. We are performing transmission lose calculations (with the PE model) with sound speeds constructed from the two-layer model simulations. Our understanding of the mode conversions at resonant frequencies has resulted in a model that uses Eq. (1) to predict the resonant frequency without running an acoustic model. This Search Algorithm for Resonance Anomalies (SARA) has been successfully applied to oceanographic soliton data taken in the Strait of Messina[8].

During the October 1995 cruise in the strait of Messina a southward propagating trains of solitons was chased 5 times and measured with a CTD chain. A northward propagating train was measured 4 times in a corresponding manner. We have extracted the temperature and salinity profiles from the data and have calculated the density and sound speed distributions. Some preliminary transmission lose calculations have been performed with the measured sound speeds using a PE model. There are indications of resonance at some of the frequencies.
 
 
 

References.

1. J. X. Zhou, X. Z. Zhang, and P. H. Rogers, "Resonant interaction of sound wave with internal solitons in coastal zone," J. Acoust. Soc. Am. 90(4), 2042-2054 (1991).

2. S. A. Chin-Bing, D. B. King, and J. E. Murphy, "Numerical simulations of lower-frequency acoustic propagation and backscatter from solitary internal waves in a shallow water environment," in Ocean Reverberation, edited by D. D. Ellis, J. R. Preston, and H. G. Urban, (Kluwer Academic Press, Dordrecht, The Netherlands, 1993).

3. D. B. King, S. A. Chin-Bing, and R. W. McGirr, "Effect of shallow water internal waves on broadband acoustic wave propagation," in Environmental Acoustics: International Conference on Theoretical & Computational Acoustics Vol. II, edited by D. Lee and M. Shultz (World Scientific Press, Singapore, 1994) p. 793-808.

4. The SWARM Group, "An overview of the 1995 SWARM shallow water internal wave acoustic scattering experiment," IEEE J. Oceanic ENG., 22(3), 465-500 (1997).

5. The Shelfbreak PRIMER Group, "Shelfbreak PRIMER - An integrated acoustic and oceanographic field study in the middle Atlantic bight," in Shallow-Water Acoustics, edited by R. Zhan and J. X. Zhou.

6. M. D. Collins, "FEPE user's guide," NORDA TN-365, Naval Research Laboratory, Stennis Space Center, Mississippi, 1988.

7. M. D. Collins, R. J. Cederberg, D. B. King, and S. A. Chin-Bing, "Comparison of algorithms for solving parabolic wave equations," J. Acoust. Soc. Am. 100, 178-182 (1996).

8. S. A. Chin-Bing, D. B. King, R. A. Zingarelli, and A. Warn-Varnas, "A Search Algorithm for Resonance Anomalies (SARA)," 1999 NRL Review, Naval Research Laboratory, Washington, DC, 1999.

9. P. Brand, A. Rubino, W. Alpers and J. Backhaus, "Internal waves in the Strait of Messina studied by a numerical model and synthetic aperture radar images from the ERS-1 Satellites," J. Phys. Oceanogr., 27(5), 648-663 (1997).

10. P. Martin, Private communication (1999).

11. F. Guo-hong, "Tides and tidal currents in East China Sea, Huanghai Sea and Bohai Sea," Oceanology of China Seas, 1, 101-112 (1994). Kluwer Academic Publishers.

12. H. Lie, "Summertime hydrographic features in the southeastern Hwanghae," Prog. Oceanog., 17, 229-242 (1986).

13. H. Essen, "Interpretation of Observed Fluctuations of the Acoustic Field in the SOFAR-Channel as Result of Internal-Wave Disturbances," PhD thesis. University of Hamburg (1976).