Acoustic Mode Coupling Within Internal Solitary Waves and Wave Groups

Timothy F. Duda and James C. Preisig
 

Applied Ocean Physics and Engineering Department
Woods Hole Oceanographic Institution, Woods Hole, MA 02543

Abstract: Propagation of sound through continental shelf internal solitary waves and wave groups (packets) is shown to be strongly influenced by coupling of the acoustic normal modes. Transfer of energy between modes (coupling) is caused by strong lateral gradients of sound speed in the waves. In the simplified situation of a symmetric individual soliton of lateral scale 50 to 400 m in 50-m deep water, the coupling behavior mimics that from from a square-well thermocline displacement. The the more realistic case of a wave group, coupling is controlled by the modal input conditions, the dimensions of each wave and of the group, and the ambient depth structures of temperature and salinity. In the case of a moving packet, changing relative mode phasing alters the coupling and the resultant signal properties as the packet moves. The mode phasing within the packet varies with time scales of minutes for a moving packet, causing coupling and signal fluctuations at comparable time scale.

Introduction

Energetic baroclinic tides and waves are a common feature of continental slope regions during stratified periods [Huthnance, 1989] These often have characteristics comparable to internal solitary wave (ISW) or ``soliton'' mathematical solutions for stratified systems. The large vertical water displacements of these waves cause significant perturbation of the acoustic waveguide, making them important contributors to fluctuations of low-frequency acoustic signals. By low frequencies, we mean those having less than 15 propagating modes in the water-column waveguide, usually less than 1000 Hz on the continental shelf. The short scale (less than 200 m) of the solitary waves and the large displacements suggest that adiabatic mode propagation (independently propagating normal modes) criteria [Milder, 1969] may be violated and energy may scatter between modes. A few studies of this coupled-mode effect in the shallow-water waveguide have been published in the last decade, starting with Zhou, Zhang and Rogers, 1991.

We have completed two studies on this topic, Preisig and Duda 1997; Duda and Preisig, 1999. The results are restricted to acoustic propagation within 65 degrees of the direction of soliton propagation. Attenuation of acoustic energy in the bottom does not influence the mode coupling behavior in ISW's. On the other hand, attenuation plays a very important role in the acoustic energy far downstream of ISW mode-coupling events. This is because the high-order modes tend to suffer more attenuation than low-order modes, and a varying blend of modes arising from coupling can lead to strong energy fluctuations.

Analysis of horizontal mode refraction within ISWs for acoustic paths oblique to the ISW troughs shows that the modeling should work for paths at angles up to 65 degrees from a path normal to the solitary wave crests. Therefore, a stretching of the effective horizontal scale of the ISW (L) by a factor of $\cos^{-1}\theta$, allows the results to be applied to a wide range of incidence angles.

This numerical work was motivated in part by the SWARM acoustic experiment east of New Jersey [Apel et al., 1997; Headrick 1997].

Single-Wave Coupling

Our initial study was of coupling within individual solitary waves. With numerically simulation of 200 and 400 Hz sound in a waveguide of 50 m depth, it was shown that the energy modal energy distribution changes rapidly at the steep faces of internal solitary waves having vertical displacement shape $\eta (x,t) = a\, {\rm sech}^2 ((x-ct)/L)$. The coupling occurs over propagation ranges of tens of meters (Figure 1), small in comparison to the so-called mode cycle distance, defined as the scale of the difference of the wavenumbers of a pair of interacting modes. For L less than about 200 m, the coupling at each face is well approximated by a sharp-interface approximation (SIA), meaning that the effect of the entire wave can be approximated well by coupling at a pair of interfaces separated by approximately L, a square-well.
 

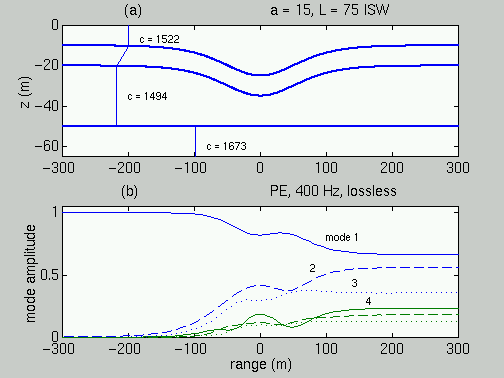
Figure 1.  The model sound-speed profile and an example soliton are shown
in the upper frame.  Below,  amplitudes of modes as a function of
position within the wave are shown.  Only mode 1 energy comes into the
wave from the left,  whereas many modes contain energy after the wave
is encountered.

Using the SIA, which involves simple propagation of normal modes except at the coupling locations, the relative phases of modes propagating through the troughs of ISW's were shown to control the amount of net mode coupling induced by the ISW. For the case examined, 400 Hz and a three-layer system, this generally holds for horizontal ISW scales of less than 200 meters (Figure 2).

The relative phase changes in the modes can be used to predict the existence of four physical regimes. ISW's of small L are in the cancellation regime of little net coupling. The net coupling regime appears for longer waves, as do periodically occurring regimes of little net coupling referred to as transparent resonances which are determined by interference of energetic modes in the trough. The fourth regime is adiabatic propagation, the long-ISW limiting case, which occurs for L above a limit which varies with mode number, stratification, etc. The cases of cancellation and transparent resonance have little or no net coupling after energy completely traverses the wave, but are distinct from the adiabatic situation because they exhibit strong coupling within the ISW.
 
 

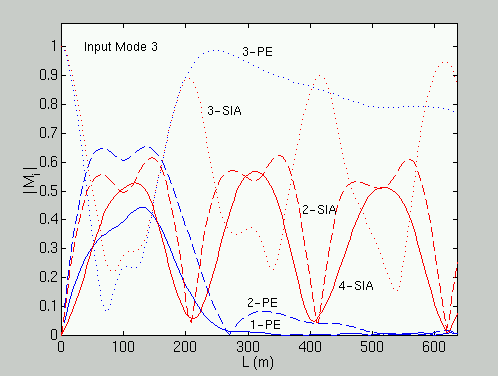
Figure 2:  Sharp interface (SIA) numerical solutions agree well with
Parabolic Equation solutions (PE) for internal waves shorter than 250 m.
The mode amplitudes after traversing single solitons of amplitude 15 m
and variable L are shown, with energy coming into the wave only in mode 3.

Coupling in Moving Wave Packets

Since solitary waves generally appear in packets rather than individually [Fu and Holt, 1984; Liu, 1988; Sandstrom and Oakey, 1995] our understanding must be extended to the effects of packets of waves. An insight from the sharp interface approximation single-wave study is that the relative phasings of the dominant modes at the scattering interfaces are the most significant factor in coupling. Earlier studies have investigated packet effects by attempting to relate the physical characteristics of packets to the induced coupling [Zhou, Zhang and Rogers, 1991; Zhou, 1993]. However, we have found that very different coupling will result from the same packet shifted a few hundred meters, with all other parameters unchanged. We have performed detailed analysis of evolving coupling behavior in a packet as it moves through the ocean. It was shown that the relative phasing between dominant modes largely controls mode coupling and signal fluctuations caused by an entire packet, comparable to single-wave behavior, despite the added complexity of the problem.

There are two basic results: (1) Solitary wave packets can cause gain or loss of acoustic energy received at ranges of order 35 km through interaction of mode coupling and attenuation of higher modes. The net gain is dependent on packet position relative to the source and source depth. (2) Superimposed on those persistent signal gains (or losses) are fluctuations having time scales of minutes. These fluctuations are controlled primarily by the relative phasings of the dominant modes of the acoustic field as it first encounters the soliton packet.
 
 

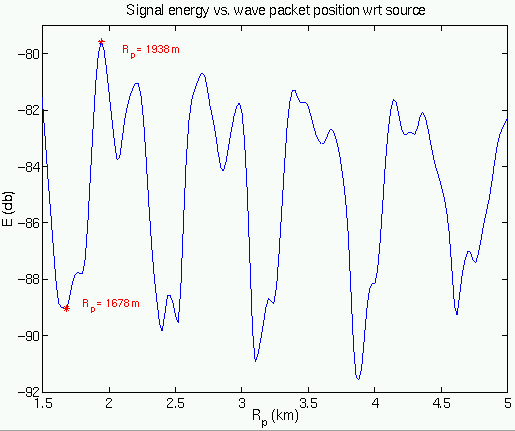
Figure 3.  The signal reaching a receiver 33 m from a source is a strong function of
the position of an intervening internal wave packet.  At packet speed 1 m/s, this represents
one hour of time.

 

Figure 3 shows depth-integrated acoustic energy in the water column, 400 Hz, after propagation through a set of three solitons at range of a few km from the acoustic source to a receiver at 33 km distance. Propagation is adiabatic except in the packet. $R_\rho$ is the x-position of the furthest crest from the source, which is at x=0. For packet speeds of roughly 1 m/s, this represents about one hour of signal fluctuation. Two situations chosen for further analysis are highlighted, one loud (position 1938 m) and one quiet (position 1678 m). Figures 4 and 5 show the level of energy in each acoustic mode between the source and the receiver. The modes are attenuated by bottom interactions at different rates. Since mode 1 propagates effectively, the loss of mode 1 energy to other modes in the $R_\rho = 1678$ case leads to signal loss at 33 km. Conversely, it is useful to compare the nonlinear-wave effects to other possible effects. A single nonlinear wave packet of 10 to 15 m displacement amplitude gives signal fluctuations of order 10 dB at 33 km range. A continuous field of small (1-3 m amplitude) thermocline displacements has an effect of roughly one dB.
 
 

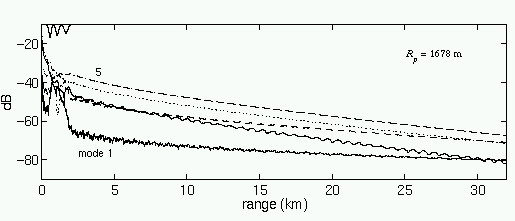
Figure 4.  Mode 1 loses energy to other modes in a soliton packet at range
1678 m from the source at range 0.  The energy which is transferred to the
higher-order modes is attenuated to a greater extend than it would have been
if it had remained in mode 1,  so the signal level at 33 km is reduced by the packet.
 
 

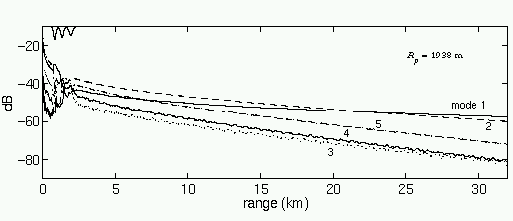
Figure 5.  Mode 1 is amplified by the wave packet at range 1978 m from the source,
then it propagates strongly to a receiver at 33 km range.  The signal is amplified by the
presence of the packet, unlike the situation with the packet at the nearby location
of Figure 4.

Summary

Analysis of mode coupling within large-displacement thermocline displacements intended to mimic the behavior of nonlinear internal waves and wave groups shows that these phenomena can have strong effects on coastal acoustic signals of a few hundred Hz. Such strong fluctuations have been seen in recent acoustics experiments including SWARM (Figure 6). Our results strongly indicate that effects of nonlinear waves are at least part of the explanation.
 
 

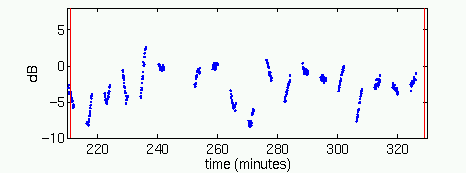
Figure 6.  400-Hz signal energy fluctuations at 33 km from the source during
the SWARM experiment on the continental shelf south of New York.

References

Apel, J. R. et al, An overview of the 1995 SWARM shallow water internal wave acoustic scattering experiment,
IEEE J Oceanic Eng.,  22, 465-500, 1997.

Duda, T. F. and J. C. Preisig, Acoustic effects of moving coastal solitary wave packets,  IEEE J Oceanic Eng., to appear, 1999.

Fu, L.-L., and B. Holt,  Internal waves in the Gulf of California: Observations from a spaceborne radar, J. Geophys. Res., 89, 2053-2060, 1984.

Headrick, R. H., Analysis of Internal Wave Induced Mode Coupling Effects on the 1995 SWARM Experiment Acoustic Transmissions,  MIT/WHOI Joint Program, PhD Dissertation, 1997.

Huthnance, J. M., Internal tides and waves near the continental shelf edge, Geophys. Astrophys. Fluid Dynamics.,
48, 81-106,  1989.

Lui, A. K.,  Analysis of nonlinear internal waves in the New York Bight, J. Geophys Res, 93, 12,317-12,329, 1988.

Milder, D. M., Ray and wave invariants for SOFAR channel propagation, J. Acoust. Soc. Am., 46, 1259-1263, 1969.

Preisig, J. C., and T.  F. Duda,  Coupled acoustic mode propagation through continental-shelf internal solitary waves,  IEEE J. Oceanic Eng..,  22, 256-269,  1997.,

Sandstrom, H., and N. S. Oakey., Dissipation in internal tides and solitary waves, J. Phys. Oceanogr., 25, 604-614, 1995.

J. Zhou, X. Zhang and P. H. Rogers, Resonant interaction of sound wave with internal solitons in the coastal zone, J. Acoust. Soc. Am., 90, 2042-2054, 1991.
 

1998-10-23