This is a portion of a paper by Porter, D. L. and D. R. Thompson, 1998, Continental shelf parameters inferred from SAR internal wave observations. J. Atmos. Oceanic Tech. In press, used with permission.
 
 
 

Continental Shelf Parameters Inferred from
SAR Internal Wave Observations


  D. L. Porter and D. R. Thompson (The Johns Hopkins University, Applied Physics Laboratory, Laurel, MD 20723; 240-228-4230; e-mail: David.Porter@jhuapl.edu 240-228-4559; email: Donald.Thompson@jhuapl.edu )
 
 
 
Abstract

This paper shows a preliminary results on the use of Synthetic Aperture Radar (SAR) imagery to extract oceanographic information about the continental shelf. The surface manifestation of internal waves is observed using the Synthetic Aperture Radar (SAR) onboard the European Research Satellite 1 (ERS-1). The depth of the pycnocline and the density of the surface layer can be estimated from the dispersion relation obtained from a two-layer fluid model. The other parameters that are required to make this estimate are obtained by assuming climatological bottom density, estimating the speed of propagation from the tidal-generated wave packets, and calculating the depth of the pycnocline based on the isobath where the internal waves are dissipated. This robust method for obtaining quantitative information about the structure of the shelf's water column shows good agreement with the in situ observations from that area.
 
 

 Results

Figure 1 is a SAR image from ERS-1 of the waters just south of central Long Island. The image is 100km on the side. The internal wave crests in this image are one tidal cycle apart, (i.e., 12.42 h) and by measuring the distance between the wave packets we can estimate their speed of propagation. Fgiure 1 shows nine lines equally spaced along the wave crests of two internal-wave trains whose generation time is assumed to be separated by 12.42 h. We have averaged the length of the nine lines and divided that by the tidal cycle period to obtain a speed of 0.62 ± 0.06 m/s, which is within the range of speeds observed in the New York Bight by Liu [1988].
 


Figure 1. Image of July 18, 1992, the upper left hand corner shows a small section of the south shore of Long Island, NY.   What does this information tell us about the density structure of the water column? From CTD measurements, conducted concurrently during JUSREX, we observe the depth of the pycnocline in the region between the two internal-wave packets was in the 20 m range with a bottom-layer density of 1.0253 gm/cm3 and an upper-layer density of 1.0224 gm/cm3. Thus the density difference between the two layers was 0.0029 gm/cm3.
 
 

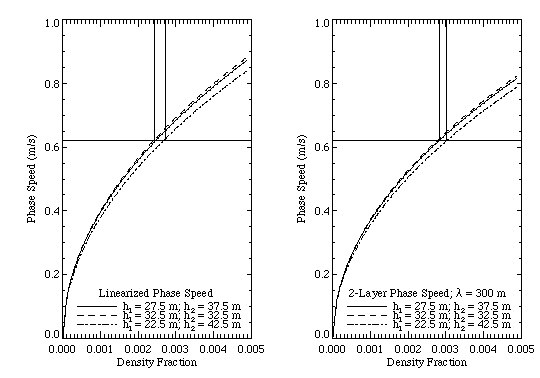
Figure 2. Phase speed vs. density fraction computed from linearized relationship (left panel), and full 2-layer dispersion relation (right panel) for several combinations of layer depths. The horizontal line shows where a phase speed of 0.62 m/s intersects the various curves, and the vertical lines indicate the error bounds on the density fraction corresponding to the depth variations.
 
 

 We have developed a procedure that uses linear wave theory to infer oceangoprhaic paramters. The assumptions and steps in this procedure are: 1.) The total depth at the position where the internal waves no longer appear in the SAR image was determined from bathymetry to be about 55 m. With the assumption that in a two-layer regime, the waves dissipate when the layer depths are equal, we deduce layer depths of 27.5 m at this position. 2.) A further assumption is that the upper-layer depth remains roughly constant over the entire region from shelf break to the dissipation location. 3.) The bathymetry at the position where the internal-wave phase speed is measured from the imagery (as discussed above in conjunction with Figure 1), then implies the lower-layer depth at this location. For the present case, the depth at the phase-speed measurement location is 65 m, which implies a bottom-layer depth of 37.5 m. 4.) We may now use the linearized phase-speed equation to determine the fractional density change, (density 2-density 1)/density; 1, between the two layers, or, if the lower-layer density is known (from climatology for example), the absolute upper-layer density. If we take the value of density2 = 1.0253 gm/cm3 measured during JUSREX, the density difference from the linearized phase-speed estimate in Figure 2 yields an upper-layer of denisty1 = 1.0228 gm/cm3 in good agreement with the estimated value of 1.0224 gm/cm3.
 
 

There are, of course, several caveats that need to be stressed in connection with discussion presented above. First of all, one must keep in mind that SAR observations are time limited. This means that an estimate of the location of the dissipation region may be in error simply because the waves haven't yet propagated further onto the shelf at the time of the image. This usually results in an over-estimate of the critical depth (and the pycnocline depth). Also, there will certainly be cases when the water column is not well characterized as a simple two-layer system. Especially near the shelf break for example, a thin but well-defined bottom layer is sometimes observed below the usual two-layers typical of the region further in shore [Lynch, et al., 1997].
 
 

CONCLUSIONS
 
 

We have shown in this paper how it may be possible to remotely estimate various properties of the water column on the continental shelf using SAR imagery in conjunction with knowledge of the local bathymetry, climatological density data, and simple models for internal-wave evolution. Theoretical studies of two-layer fluids indicate that dissipation of internal waves impinging on shoaling water occurs when the depth of the bottom layer, which is decreased by the shoaling, becomes equal to that of the upper layer. Using this idea, we have determined this critical depth for a particular case study by noting the location in the SAR image where the internal-wave surface signatures disappear. The depth of each layer at this position is then half the total depth. By assuming that the internal waves are generated at the shelf break on each diurnal tidal cycle, we have also estimated their phase speed by measuring the distance between successive packets in the image. With this information along with the 2-layer dispersion relation, we have been able to estimate the fractional density change between the two layers. Furthermore, an estimate of the surface density is possible by using the climatological bottom density. We have compared the parameters extracted using these methods with in situ measurements collected concurrently with the SAR imagery. This comparison showed good agreement, and gives us confidence that our techniques are robust.

REFERENCES

Liu, A. K., 1988: Analysis of Nonlinear Internal Waves in the New York Bight. J. Geophys. Res., 93, 10, 12 317-12 329.
 
 

Lynch, J. F., G. G. Gawarkiewicz, C. S. Chiu, R. Pickart, J.H. Miller, K. B. Smith, A. Robinson, K. Brink, R. Beardsley, B. Sperry, G. Potty, 1997: Shelfbreak PRIMER - An Integrated Acoustic and Oceanographic Field Study in the Middle Atlantic Bight. Proceedings: Shallow Water Acoustics Conference, Beijing, China, (in press).