How to Describe Strong Internal Waves in Coastal Areas

Lev A. Ostrovsky

University of Colorado, CIRES; NOAA ETL
Boulder, CO, USA.

Abstract

Model evolution equations for strongly nonlinear internal waves in the ocean are discussed in application to recent field experiments including COPE. For the cases considered, a commonly used Korteweg-de Vries (KdV) equation is inapplicable, and modified models with adding higher-order terms are needed (CombKdV equation). A most adequate and physically substantiated model uses an ``exact'' (for very long waves) nonlinearity and nonlinear dispersion. Theoretical results are compared with observational data. Some problems are discussed in conclusion.

Introduction

There exists a relatively large body of literature concerning observations and theoretical models of nonlinear internal waves (IW) in shelf areas (see, e.g., the review paper [1]). A common tool for description of these processes is the Korteweg-de Vries (KdV) equation that is applicable to relatively small-amplitude waves. However, in some cases really strong nonlinear waves are observed. A recent example is the Coastal Ocean Probe Experiment (COPE), which has been carried out in September 1995 in the Oregon Bay. Its data clearly indicated the presence of extremely strong trains of tidally-generated internal waves [2],[3]. The isotherm depressions consisted of solitary pulses (we shall call them solitons independently of how strict this definition could be) with amplitudes of thermocline displacements typically of order 10-20 m, and sometimes reaching 30 m. Even more important is the fact that they propagate into the background of a very shallow, 5-7m depth, pycnocline. This testifies for an extremely strong nonlinearity of the process (a high ``Mach number,'' using the gas dynamic terminology). Thus, the problem of creating an adequate theoretical model of these processes is evidently actual.

KdV model

As mentioned, the models of shallow-sea solitons are commonly based on the classical Korteweg-de Vries equation
 
 

$$\frac{\partial \eta }{\partial \tau }+\left( c+\alpha \eta \r......artial x}+\beta \frac{\partial ^{3}\eta }{\partial x^{3}}%=0,$$ (1)

where $\eta$ is the displacement of an isopycnal surface, and c is the phase velocity of a long wave corresponding to a given mode. This parameter is defined as an eigenfunction of the corresponding linear boundary problem for long-wave limit. Here we shall consider a simplified model of stratification in which the fluid consists of two layers: upper, of thickness h₁ and density $\rho_1$ and lower, with h₂ and $\rho _{2}>\rho _{1},$ respectively. In this case, the parameters of $\left(\ref{d1}\right)$ are
 
 

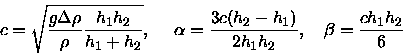$$c=\sqrt{\frac{g\Delta \rho }{\rho }\frac{h_{1}h_{2}}{h_{1}+h_......_{2}-h_{1})}{2h_{1}h_{2}},\quad \beta =\frac{ch_{1}h_{2}}{%6}$$ (2)

(all these expressions suggest that $\Delta \rho =\rho _{2}-\rho _{1}<<\rho_{1,2}$ which is always true in the ocean). This equation has a family of well known solitary solutions. Such a model works well for a number of IW observations but is inapplicable for the cases considered here.

CombKdV model

The next-level model which may be tried takes into account the higher degree on nonlinearity; it is so-called CombKdV equation [1]:
 
 

$$\frac{\partial \eta }{\partial \tau }+\left( c+\alpha \eta +\......partial x}+\beta \frac{\partial ^{3}\eta}{\partial x^{3}}=0,$$ (3)

The parameters c, $\alpha ,$ and $\beta$ are the same as for the KdV equation. for $\alpha _{1}=0.$ The cubic nonlinearity parameter $\alpha _{1},$ for a two-layer model, is
 
 

$$\alpha _{1}=\frac{3c}{h_{1}^{2}h_{2}^{2}}\left[ \frac{7}{8}\l......ft( \frac{h_{1}^{3}+h_{2}^{3}}{h_{1}+h_{2}}%\right) \right] .$$ (4)

Note that always $\alpha _{1}<0,$ whereas the sign of $\alpha$ depends on the position of the interface (pycnocline). In our case h₁<h₂, and $%\alpha <0$ as well, so that in the solitary wave, $\eta <0$( a depression). Moreover, there exist a critical value of displacement $\eta ,$ for which the nonlinearity tends to zero, namely: $\eta _{m}=-\alpha /\alpha _{1}$.

The equation $\left( \ref{eq:1}\right)$ is known to be completely integrable. It also has a solution in the form of a soliton. Its amplitude $%\eta _{0}$ is limited by the value $\eta _{cr}=\alpha /\alpha _{1}.$ If $%\eta _{0}$ is sufficiently small, the wave is close to that defined by the KdV equation, but for larger solitons, the wave is broadening and when $%\eta _{0}$ approaches $\eta _{cr}$, it acquires almost rectangular shape.

Comparison with the experimental data shows that the CombKdV model gives a much better agreement than the usual KdV model.

An equation with ``exact'' nonlinearity and nonlinear dispersion.

A more consistent approach can be developed based on the expression for ``exact'' nonlinear term obtained as an analog of the shallow-water theory for the surface waves. We suggest to use the equation
 
 

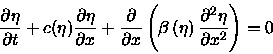$$\frac{\partial \eta }{\partial t}+c(\eta )\frac{\partial \eta......ta \right) \frac{\partial^{2}\eta }{\partial x^{2}}\right) =0$$ (5)

with the same $c\left( \eta \right)$ and $\beta (\eta )$ depending on the local pycnocline displacement: in particular,
 
 

$$\beta =\frac{c(\eta )}{6}\left( h_{1}+\eta \right) \left( h_{2}-\eta \right).$$ (6)

In case of a thin upper layer most of wave energy is concentrated in this layer, and the local long-wave velocity is
 
 

$$c\left( \eta \right) =\sqrt{g^{\prime }}\left( 3\sqrt{h_{1}+\......qrt{%h_{1}}\right) ; \quad g^{\prime }=g(\Delta \rho /\rho ).$$ (7)

For arbitrary relationship between h₁ and h₂, the local wave velocity must be found from differential equations (D. Pelinovsky):
 
 

$$c=H^{-1}\left[ \frac{\left( h_{2}-\eta \right) ^{2}-\left( h_...... -\frac{H^{2}\left( h_{1}+\eta\right) }{h_{2}}u^{2}}\right] ,$$ (8)

$$\frac{du}{d\eta }=\frac{c\left( \eta \right) +u}{h_{1}+u}$$ (9)

The equation $\left( \ref{eq:bb}\right)$ also has a family of solitons which fit the COPE data quite well. It is notable that there exist a rather wide intermediate range where the soliton duration is almost independent of its amplitude; this agrees well with observational data [2].

Conclusions

These results show that even for strongly nonlinear waves, one-dimensional evolution equations, albeit not strictly derived from the basic hydrodynamic equations, can provide a satisfactory description of real processes in a broad range of their parameters. Now we are continuing to actively study evolution equations with nonlinear dispersion.

It appears that strongly nonlinear internal waves are a rather typical phenomenon for some shelf areas during spring tides; note that the PRIMER experiment performed by WHOI near the East coast, also demonstrated the presence of strong IWs. These areas deserve a special attention of oceanographers as those of especially active mixing, transport of biomasses and pollutants, etc. Regarding the theory, it is very desirable, along with further studies of model equations, to supplement these studies with direct numerical modeling of hydrodynamic equations.
 

1998-10-08