
Patrick Lynett and Philip L.-F. Liu
School of Civil and Environmental Engineering
Cornell University
Ithaca, NY
Internal waves have been observed in different parts of the world. For example, Ziegenbein (1969) and Lacombe & Richez (1982) measured eastward propagating internal waves in the Strait of Gibraltar. LaViolette & Arnone (1988) presented further measurements of internal waves in the Strait, together with simultaneous visual observations from aircraft and the space shuttle. The internal waves are believed to be generated by the tidal flow over Camarinal Sill at the western end of the Strait. While the tidal flow over the sill is westward, an internal lee wave or a hydraulic jump is formed on the westward side of the sill. As the westward component of the flow relaxes and eventually reverses to an eastward flow, the lee wave disturbance evolves into a train of nonlinear internal waves propagating eastward into the Strait.
Gargett (1976) studied internal waves observed in the Strait of Georgia, British Columbia. She attributes their generation to abrupt changes in current speed, characteristics of the tidal flow within the passes between islands to the south of the strait.
Farmer & Smith (1978) measured trains of large amplitude, nonlinear internal waves in Knight Inlet, a long and narrow fjord in British Columbia. These waves typically had amplitudes in excess of 10 meters and wavelengths of 70 to 100 meters. They traveled on the pycnocline, whose depth was typically 15 to 30 meters in the 400 meters deep water.
Osborne & Burch (1980) recorded the observation of internal waves in the Andaman Sea, offshore Thailand. Their measurements indicated a connection with the semidiurnal tide and suggested that the Nicobar Island chain and northern Sumatra were likely candidate for potential source regions. Osborne & Burch (1980) noted that knowledge of internal wave behavior would be necessary for the design of deepwater offshore production facilities.
More recently, using the ERS-1 and ERS-2 SAR images, Liu et al. (1998) reported many observations of internal waves in China Sea. They attribute the frequent generation of internal waves in the region of northwest of Taiwan to the upwelling induced by the Kuroshio intrusion (major western boundary current of the Pacific) at the Shelf break. They also showed the evidences of strong wave-wave interactions in both Yellow Sea and East China Sea.
Most of existing analyses on the propagation of internal waves have been based on the Korteweg de Vries (KdV) equation, neglecting two-dimensional and reflection effects (Lee & Beardsley 1974, Farmer 1978, Maxworthy 1979, Apel et al. 1985, Liu 1988), or the Kadomtsev-Petviashvili (KP) equation, which includes weak two-dimensional effects (Pierini 1989, Tomasson 1991, Chen & Liu 1995). However, the observations made in China Sea clearly indicated strong wave-wave interactions and the diffraction and refraction of internal waves by bathymetry and islands (Liu et al. 1998). Therefore, two-dimensional and reflection effects can not be ignored.
Tomasson (1991) derived a set of Boussinesq equations for a two-layer
fluid system. In the dimensionless form these equations can be written
as:

in which h1 and h2 are the dimensionless thickness of the upper and lower layer, respectively, (u,v) represents the flux in the lower layer, eta denotes the interfacial displacement. These equations are derived under the assumption of weak nonlinearity, alpha << O (1), and weak dispersion, beta << O (1). It is also assumed that O(alpha2)=O(beta). Note that for completeness, both quadratic nonlinearity and cubic nonlinearity have been kept in the equations.
If the cubic nonlinear terms are ignored in the above equations can be simplified to the well-known KdV equation, which has the dimensional solitary wave solution,
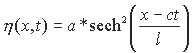
where
a = wave amplitude,
![]() ,
,
![]() ,
,
g = gravity,
![]() =
density difference,
=
density difference,
![]() ,
,
and
![]()
The analytical solution has been plotted in Figure 1.
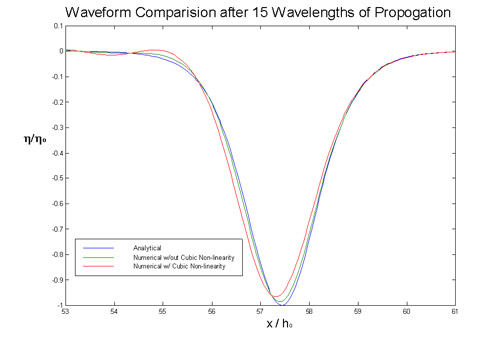
Figure 1. Solitary waveform comparison (alpha=0.1, beta=0.008) showing
analytical (blue),
numerical without cubic non-linearity (green), and numerical with cubic
non-linearity (red)
A numerical algorithm has been developed to solve the Boussinesq equations
as an initial boundary-value problem. As a test case the solitary wave
solutions are used as the initial condition and computations are carried
out with and without the cubic nonlinearity. As shown in Figure 1, after
a propagation distance of 15 wavelengths, the numerical solitary wave solutions,
without including the cubic nonlinearity, remain very similar to the analytical
solutions. However, when the cubic nonlinearity is included, the wave amplitude
is reduced slightly and the waveform is also dispersed. In Figure 2, the
evolution of a solitary wave propagating onto a shelf is displayed. In
this case the thickness of the lower layer has been decreased gradually;
the initially depressed (negative) soliton degenerates into a series of
oscillatory waves with a leading depression wave.
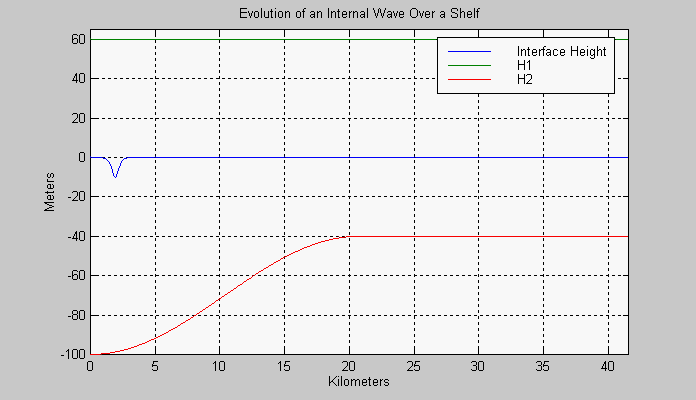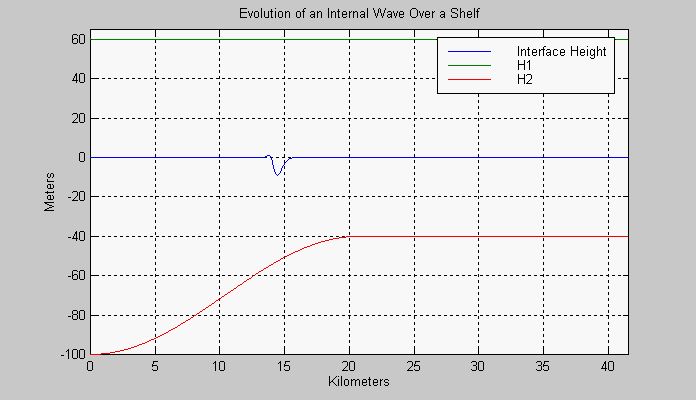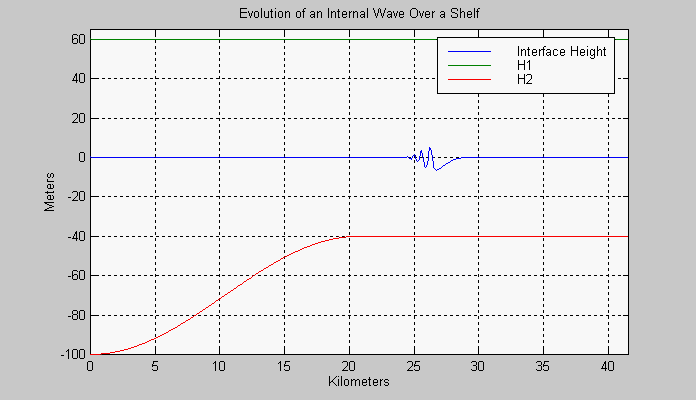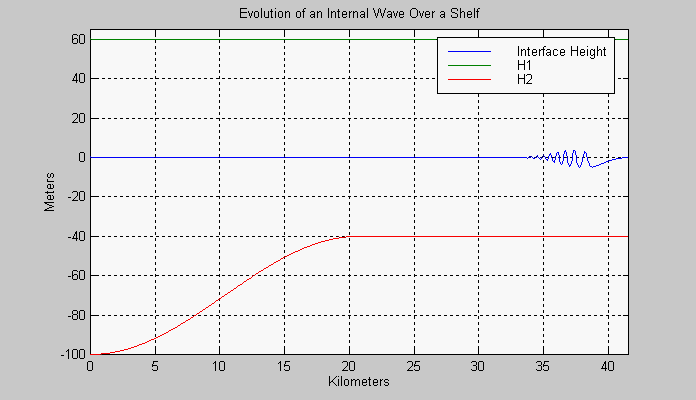
Figure 2. Internal solitary wave (alpha=0.27, beta=0.012) propogation over a shelf
The numerical model has also been used to investigate the wave-wave interactions. As shown in Figures 3 and 4, two solitons propagate obliquely at 45 and 20 degree angles, respectively. For the small incident angle case, stem waves are generated in both surface and internal waves
A B
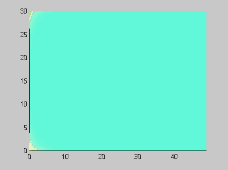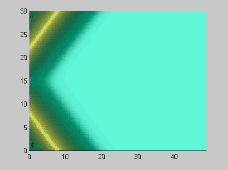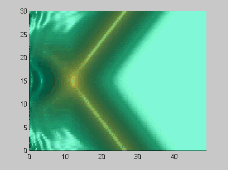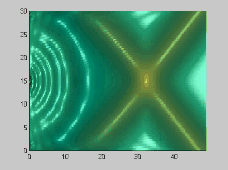
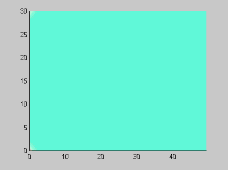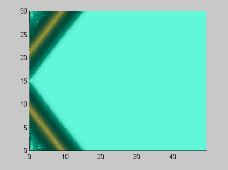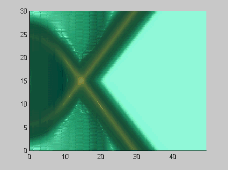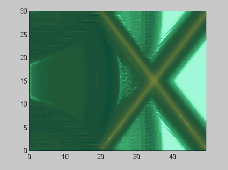
Figure 3. Wave-wave interactions for two 45 degree oblique solitary
surface waves
(alpha=0.1)[A] and internal waves (alpha=0.1,beta=0.008)[B]
A
B

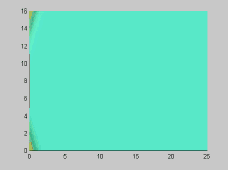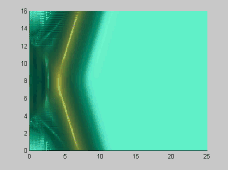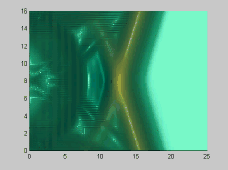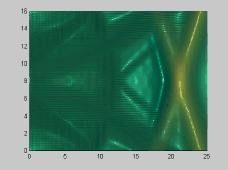
Figure 4. Wave-wave interactions for two 20 degree oblique solitary
surface waves
(alpha=0.1)[A] and internal waves (alpha=0.1,beta=0.008)[B]
From the above figures, it is evident that there are small, but clear
differences between surface and internal wave-wave interactions. The presented
numerical model will be extended to study internal wave interaction with
islands and varying topography.
References:
Chen, Y. & Liu, P. L.-F. 1995 "The unified Kadomtsev-Petviashvili equation for interfacial waves", J. Fluid Mech., 288, 383-408.
Farmer, D. M. 1978 "Observations of long nonlinear internal waves in a lake", J. Phys. Oceanography, 8, 63-73.
Lacombe, H. & Richez, C. 1982 "The regime of the Strait of Gibraltar," in Hydrodynamics of semi-enclosed seas, 13-73, Elsvier.
LaViolette, P. E. & Arnone, R. A. 1988 "A tide-generated internal waveform in the western approaches to the Strait of Gibraltar," J. Geophys. Res., 93, 15,653-667.
Lee, C-Y. & Beardsley, R. C. 1974 "The generation of long nonlinear internal waves in a weakly stratified shear flow," J. Geophys. Res., 79, 453-462.
Liu, A. K 1988 "Analysis of nonlinear internal waves in the New York Bight," J. Geophys. Res. 93, 12,317-329.
Liu, A. K., Chang, Y.S., Hsu, M. K. & Liang, N. K., 1998 "Evolution of nonlinear internal waves in East and South China Seas", J. Geophys. Res., 103, 7995-8008.
Maxworthy, T. 1979 "A note on the internal solitary waves produced by tidal flow over a three-dimensional ridge", J. Geophys. Res., 84, 338-346.
Osborne, A. R. & Burch, T. L. 1980 "Internal solitons in Andaman Sea," Science, 208, 451-460.
Pierini, S. 1989 "A model for the Alboran Sea internal solitary waves," J. Phys. Oceanography, 19, 755-722.
Tomasson, G. G. 1991 Nonlinear waves in a channel: Three-dimensional and rotational effects. Doctoral Thesis, M.I.T.
Ziegenbein, J. 1969 "Short internal waves in the Strait of Gibraltar",
Deep
Sea Res., 16, 479-487.