THEORETICAL DESCRIPTIONS OF SHALLOW-WATER SOLITARY
INTERNAL WAVES: COMPARISONS WITH FULLY NONLINEAR WAVES
Kevin G. Lamb
Department of Applied Mathematics, University of Waterloo
Waterloo, Ontario, Canada
N2L 3G1
Two formulations of shallow-water weakly nonlinear theory for internal waves are presented. The structure of solitary waves predicted by these two theories are compared with fully nonlinear solitary waves.
Introduction
In this talk two different formulations of shallow-water, weakly-nonlinear
theory will be considered and the predicted structure of solitary waves
will be compared with fully nonlinear solitary waves. The latter are computed
numerically using an iterative method (1). The two formulations of the
theory are obtained by using different sets of independent variables. For
the Eulerian formulation the independent variables are (x,z,t)
where x and z are the horizontal and vertical Cartesian coordinates
and t is time (2,3). For the Euler-Lagrange formulation of the theory
z
is replaced by the Lagrangian coordinate ![]() where
where ![]() is the vertical displacement of the fluid particle at (x,z,t)
from its rest position (4).
is the vertical displacement of the fluid particle at (x,z,t)
from its rest position (4).
Eulerian Formulation
Making the incompressible and Boussinesq approximations, neglecting
rotation and viscosity, the equations of motion in Cartesian coordinates
are
![]()
where![]() is the stream function for the velocity
is the stream function for the velocity ![]() ,
, ![]() where g=9.81 ms-1is the constant gravitational acceleration,
where g=9.81 ms-1is the constant gravitational acceleration, ![]() is a constant reference density and
is a constant reference density and ![]() is the density perturbation due to the wave, and
is the density perturbation due to the wave, and ![]() is the Laplacian operator. The buoyancy frequency N(z) is
given by
is the Laplacian operator. The buoyancy frequency N(z) is
given by
| (2) |
where ![]() is the undisturbed density field. For simplicity it is assumed that there
is no background flow. The fluid is assumed to lie between two horizontal,
rigid planes at
z=0,H so that the boundary conditions are
is the undisturbed density field. For simplicity it is assumed that there
is no background flow. The fluid is assumed to lie between two horizontal,
rigid planes at
z=0,H so that the boundary conditions are ![]() at
z=0,H.
at
z=0,H.
Under the assumption of small, long waves an asymptotic expansion of the above equations leads to a weakly-nonlinear solution of the form
![\begin{displaymath}\begin{split}\begin{pmatrix}\psi \\ [-2mm] _{b}\\ \overline{......{0,2} \end{pmatrix} \biggr\} + \cdots \, .\end{split} \tag{3}\end{displaymath}](img13.gif) |
(3) |
Here B = B(x,t)
and the ![]() and E with the various indices are functions of z.
and E with the various indices are functions of z. ![]() is a parameter whose value we take to be one. Nondimensional equations
would have the same form, in which case
is a parameter whose value we take to be one. Nondimensional equations
would have the same form, in which case ![]() appears as a small parameter measuring the strength of the nonlinearity
and dispersion. Here it is included to indicate the relative ordering of
the various terms. The leading-order terms in (3) describe infinitesimal,
long waves. These, together with the
appears as a small parameter measuring the strength of the nonlinearity
and dispersion. Here it is included to indicate the relative ordering of
the various terms. The leading-order terms in (3) describe infinitesimal,
long waves. These, together with the ![]() terms, comprise first-order theory. Second-order theory includes the
terms, comprise first-order theory. Second-order theory includes the![]() terms.
terms. ![]() and the linear long-wave propagation speed c are given by the eigenvalue
problem
and the linear long-wave propagation speed c are given by the eigenvalue
problem
| (4) |
with boundary conditions ![]() .
Only mode-1 waves are considered so c is the largest eigenvalue
of (4) with
.
Only mode-1 waves are considered so c is the largest eigenvalue
of (4) with ![]() the corresponding eigenfunction. The
Ei,jq
can be expressed in terms of the
the corresponding eigenfunction. The
Ei,jq
can be expressed in terms of the ![]() which
are determined by equations of the form
which
are determined by equations of the form
| (5) |
where Si,jq is
a known function of the lower-order vertical structure functions. The general
solution includes an undetermined constant multiple of ![]() (see 3). The constants rijq are determined by the solvability
conditions
(see 3). The constants rijq are determined by the solvability
conditions ![]() .
The first-order constants r10 and r01are
given by
.
The first-order constants r10 and r01are
given by
| (6) |
where
| (7) |
The second order constants are
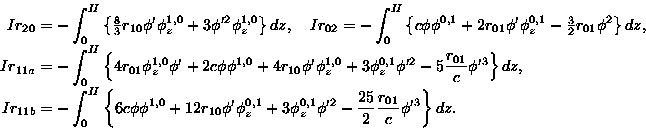 |
(8) |
The theory also yields an evolution equation for B(x,t), namely
| (9) |
To ![]() this is the KdV equation.
this is the KdV equation.
Euler-Lagrange Formulation
To use the Lagrangian coordinate ![]() as the independent variable instead of z we must be able to solve z
= z(x,y,t) for y. This requires that
as the independent variable instead of z we must be able to solve z
= z(x,y,t) for y. This requires that ![]() and in particular rules out waves with overturning isopycnals. The governing
equations (1a)-(1b) are replaced by
and in particular rules out waves with overturning isopycnals. The governing
equations (1a)-(1b) are replaced by
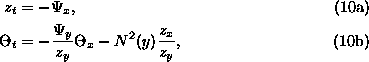
where![]() and
and ![]() are the streamfunction
are the streamfunction ![]() and vorticity
and vorticity ![]() expressed as functions of (x,y,t).
expressed as functions of (x,y,t).
Solutions of (10a)-(10b) have the form
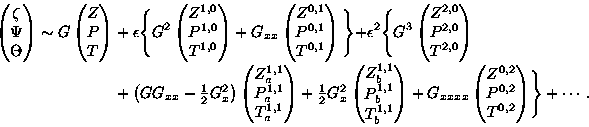 |
(11) |
where ![]() is the isopycnal displacement written as a function of y, G
= G(x,t), and Z, P and T with
the various indices are functions of y. G(x,t)
satisfies (9) with identical values for the coefficients. Z and
is the isopycnal displacement written as a function of y, G
= G(x,t), and Z, P and T with
the various indices are functions of y. G(x,t)
satisfies (9) with identical values for the coefficients. Z and ![]() satisfy the same eigenvalue problem so, if they are both scaled to have
a maximum value of 1, they are identical. In that case we can take B=G.
The remaining vertical structure functions can be expressed in terms of
the
satisfy the same eigenvalue problem so, if they are both scaled to have
a maximum value of 1, they are identical. In that case we can take B=G.
The remaining vertical structure functions can be expressed in terms of
the ![]()
Comparisons with fully-nonlinear waves
The theoretical approximations are now compared with fully nonlinear waves. Two different density profiles are considered in a fluid of depth H=100 m. The first,
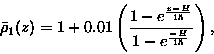 |
(12) |
has an exponentially increasing stratification. The second,
| (13) |
has a well defined pycnocline 20 m below the surface. The bottom to
surface density difference is 0.01 in both cases. For both stratifications
the wave half-widths are approximately 100 m for the largest waves. Comparisons
of the isopycnal displacement along the vertical line through the centre
of a number of waves are shown in figures 1 and 2. Solid curves are profiles
from the fully nonlinear waves. Dashed curves are the theoretical profiles.
In the Euler-Lagrange formulation the leading order isopycnal displacement
is ![]() .
For the Eulerian formulation the isopycnal displacement is obtained by
expanding
.
For the Eulerian formulation the isopycnal displacement is obtained by
expanding ![]() which gives
which gives ![]() at leading-order. Since
at leading-order. Since ![]() both expression have the identical form however there is a crucial difference
between the two. In the Eulerian expression
both expression have the identical form however there is a crucial difference
between the two. In the Eulerian expression ![]() is
the vertical displacement of an isopycnal as a function of the displaced
isopycnal height. In the Euler-Lagrange expression the vertical displacement
of an isopycnal is given as a function of the rest height of the isopycnal.
In figure 1 it can be seen that for density 1 the Eulerian description
is much better than the Euler-Lagrange description while figure 2 shows
that the opposite is true for density 2. Using first-order theory the theoretical
isopycnal profiles obtained using the Eulerian formulation are almost indistinguishable
from the fully-nonlinear wave profiles. This is remarkable as the largest
wave considered is very close to breaking (i.e.,
is
the vertical displacement of an isopycnal as a function of the displaced
isopycnal height. In the Euler-Lagrange expression the vertical displacement
of an isopycnal is given as a function of the rest height of the isopycnal.
In figure 1 it can be seen that for density 1 the Eulerian description
is much better than the Euler-Lagrange description while figure 2 shows
that the opposite is true for density 2. Using first-order theory the theoretical
isopycnal profiles obtained using the Eulerian formulation are almost indistinguishable
from the fully-nonlinear wave profiles. This is remarkable as the largest
wave considered is very close to breaking (i.e., ![]() is close to 1). Use of first-order theory for density 2 also reduces the
error significantly but the agreement is not as good. For density 2 the
largest wave is far from breaking.
is close to 1). Use of first-order theory for density 2 also reduces the
error significantly but the agreement is not as good. For density 2 the
largest wave is far from breaking.
In figures 3 and 4 vertical profiles of the horizontal velocity through the centre of the waves are shown. Solid curves are the profiles for the fully-nonlinear waves. Dashed profiles are the theoretical results. In figure 3 leading- and first-order Eulerian approximations are shown for density 1. In figure 4 leading- and first-order Euler Lagrange approximations are shown for density 2. For the Eulerian formulation the first-order velocity is given by
| (14) |
For the Euler-Lagrange formulation u is given, at first-order, by
| (15) |
For leading-order theory the ![]() terms are dropped. For the first-order expressions for u the value
of Bxx is needed in the centre of the wave. For this
the well-known solitary wave solution
terms are dropped. For the first-order expressions for u the value
of Bxx is needed in the centre of the wave. For this
the well-known solitary wave solution ![]() of the KdV equation is used to express Bxx(0,0)
in terms of bo. Here
of the KdV equation is used to express Bxx(0,0)
in terms of bo. Here ![]() at the wave centre. For the vertical profiles the second-order coefficients
r20,
r11a,
r11b
and r02 are not required, however for horizontal profiles
they are required to calculate
at the wave centre. For the vertical profiles the second-order coefficients
r20,
r11a,
r11b
and r02 are not required, however for horizontal profiles
they are required to calculate ![]() corrections
to
corrections
to ![]() and to the expression for B.
and to the expression for B.
For density 1 the theoretical estimate is very good for even the largest wave. For density 2 the magnitude of the velocities is underestimated for the larger waves well below the pycnocline. The theory does correctly predict a minimum in uimmediately below the pycnocline, something that is not predicted by leading-order theory. The Eulerian formulation incorrectly predicts a subsurface maximum in u for the largest 2 waves (not shown).
These results show that the best formulation of shallow-water weakly-nonlinear
theory for solitary internal waves is stratification dependent. Comparisons
for more complicated stratifications taken from oceanographic observations
will be shown.
References
(1) Turkington, B., Eydeland, A., and S. Wang, Stud. Appl. Math., 85, 93-127, 1991.
(2) Benney, D. J., J. Math. Phys., 45, 52-63, 1966.
(3) Lamb, K. G., and L. Yan, J. Phys. Oceanogr., 26, 2712-2734, 1996.
(4) Gear, J. A., and R. Grimshaw, Phys. Fluids.
26, 14-29,
1983.
Figures ...
1998-09-17