Flows in Rotating Channels:
Hydraulic Adjustment, Jumps and Shocks
K. R. Helfrich and L. J. Pratt
Department of Physical Oceanography
Woods Hole Oceanographic Institution
Woods Hole, MA 02543
1. Introduction
Nonlinear internal waves are common features of straits and are a consequence
of the complicated interaction of time-dependent stratified flow with topographic
features. These underlying flows are themselves highly nonlinear (typically
hydraulically controlled) and exhibit significant spatial and temporal
variation. Thus a full understanding of internal solitary wave propagation
must include an understanding of the underlying flow which both generates
and affects the evolution of the waves. In this short contribution we describe
some results of two related problems which address the nonlinear dynamics
of flow in rotating channels. The first is an extension of the dam break
problem to the case of a rotating channel (Rossby adjustment in a channel).
The second is the extension of Long's classic study of upstream influence
and hydraulic adjustment over topography to flows in a rotating channel.
In both examples we rely on solutions of the single layer shallow water
equations and therefore do not model the nonhydrostatic effects which lead
to solitary waves. However, the fully nonlinear shocks and hydraulic jumps
which do arise are resolved and described.
2. Rossby Adjustment in a Channel
The setting for the dam break problem is a rectangular channel of width w. A cross-channel (y-direction) barrier separates two semi-infinite regions of homogeneous fluid of different depths. At time t = 0 the barrier is destroyed causing the upper fluid to intrude into the shallower fluid and the formation of a leading shock, or bore. The hydrostatic solution for no rotation is given by Stoker (1957). Gill (1976) examined the linear limit when rotation is included. A steady current is set up by Kelvin waves moving away from the barrier position. The Kelvin wave moving into the shallower layer is trapped to the right-hand wall (looking in the direction of the shallow layer) while the Kelvin wave moving into the deeper layer is trapped to the left wall. The steady flow approaches the section of the initial barrier along the left wall, crosses the channel at that section, and continues along the right wall.
When the initial depth difference is finite and rotation is included,
the Kelvin wave moving into the shallow layer is replaced by a Kelvin bore.
Because of the uncertainty of the proper shock-joining conditions and non-conservation
of potential vorticity across the shock, an analytical solution to this
problem has not been found. Thus we employ numerical methods to study the
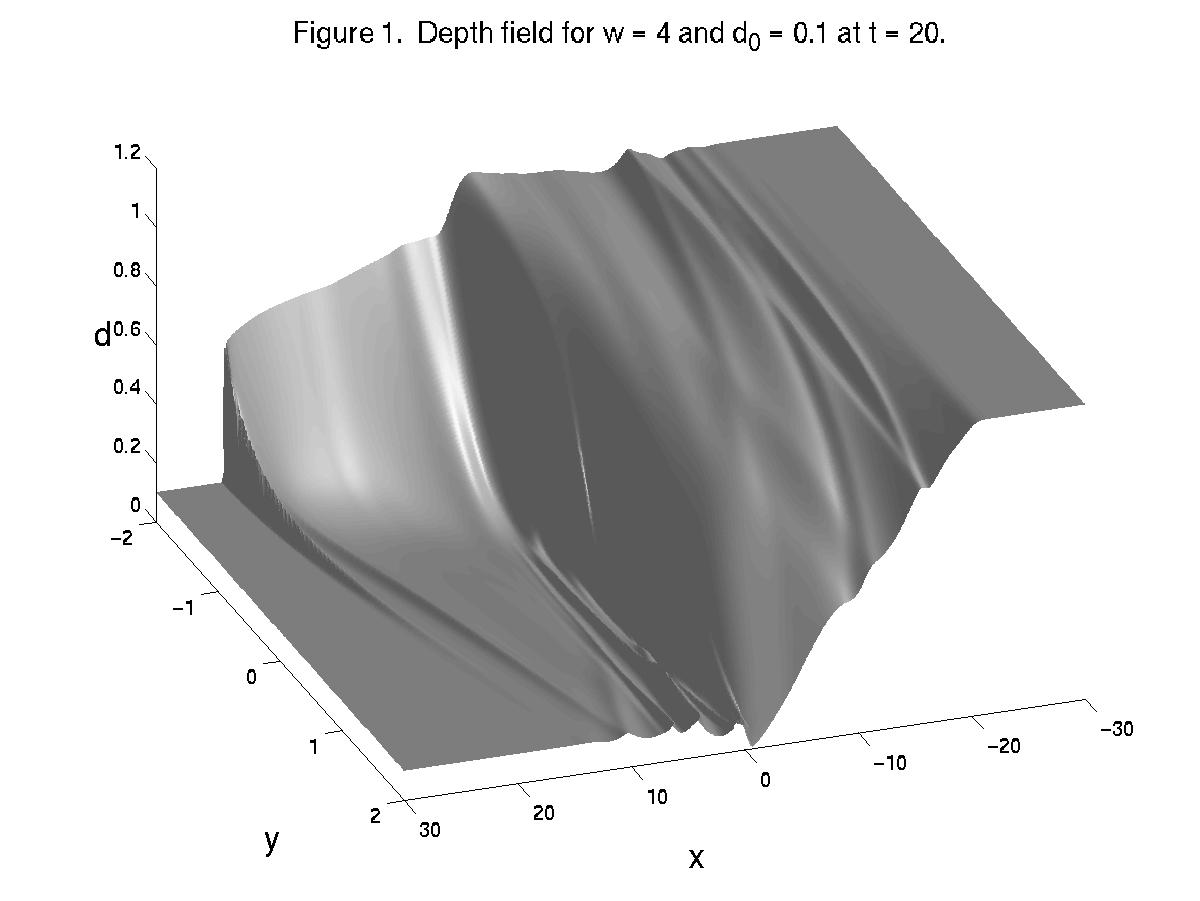
flow. Figure 1 shows a the depth field for a channel of nondimensional
width w = 4 and an initial nondimensional depth in the shallow section
d0
= 0.1, which is scaled by the initial depth in the deep region D.
The horizontal dimensions are normalized by the deformation radius based
on D. The flow is shown at t = 20. In this example the leading
shock curves back upstream and its amplitude decays away from the right
wall. Trailing the bore is a geostrophic boundary current. Near
x
= 0 there is a cross-channel geostrophic current due to the along channel
gradient in depth.
Figure 1
In a narrower channel the shock structure is rather different. Figure 2 shows a case with w = 1 and d0 = 0.25. The leading bore is now nearly straight across the channel. The amplitude decays away from the right wall (y = -0.5), but increases near the left wall. Trailing the bore near the left wall is a packet of Poincaré waves. These waves appear to be generated by the resonant mechanism described by Tomasson and Melville (1992).
We find that the leading bore extends across the channel to attach at
the left wall (within one deformation radius of its position on the right
wall) when the channel width scaled by the deformation radius in the upstream
region, w d0-1/2,
is less than about 3. In all cases the shock is connected to the following
geostrophic current by an ageostrophic boundary layer characterized by
a strong transverse jet. Shock amplitudes, measured on the right wall,
and shock speeds increase above the nonrotating solutions as w is
increased for a given d0. However, the relation between
bore speed and amplitude branches below the nonrotating relation as w
(rotation) is increased. Finally, the potential vorticity jump across the
shock is shown to depart significantly from the pseudo-inviscid estimates
due to the viscous flux of vorticity, an effect that is at best crudely
parameterized and poorly understood.
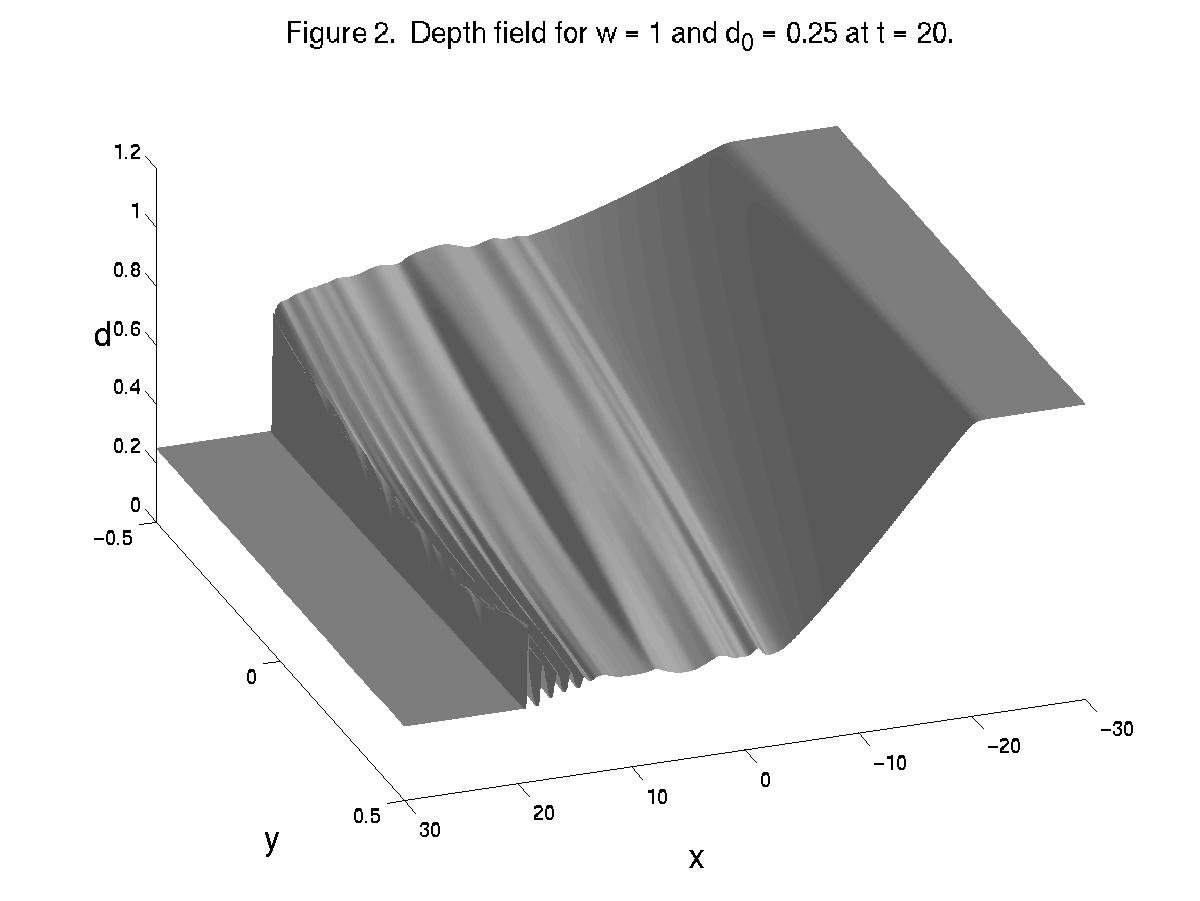Figure 2
3. Long's Problem in a Rotating Channel
In Long's (1954, 1970) classic problem on upstream influence a topographic feature is rapidly grown into a nonrotating, hydrostatic, single layer flow. The response of the fluid, and in particular the development of upstream influence, can be determined by the location of the flow in the F - hm plane, where F is the Froude number of the initial flow and hm is the final height of the topography. Upstream influence occurs through the propagation of a shock, or bore, which causes a permanent change in the flow approaching the obstacle. At the crest of the obstacle the flow is critical and downstream a hydraulic jump back to subcritical flow may exist. In the weakly nonlinear and dispersive limit the upstream influence is achieved by the radiation of a train of solitary waves (e.g., Grimshaw and Smyth, 1986).
Using the semigeostrophic approximation and the assumption of uniform
potential vorticity a theory is developed which gives the critical obstacle
height above which upstream influence and hydraulic control at the topographic
crest is achieved for rotating flow in a uniform channel. The critical
height is a function of the initial flow Froude number (defined using the
appropriate characteristic speeds in the rotating system) and the channel
width relative to the deformation radius based on the upstream potential
depth. The structure of the critical height curve is similar to the nonrotating
version with increasing critical height as F increases above, or
decreases below, one.
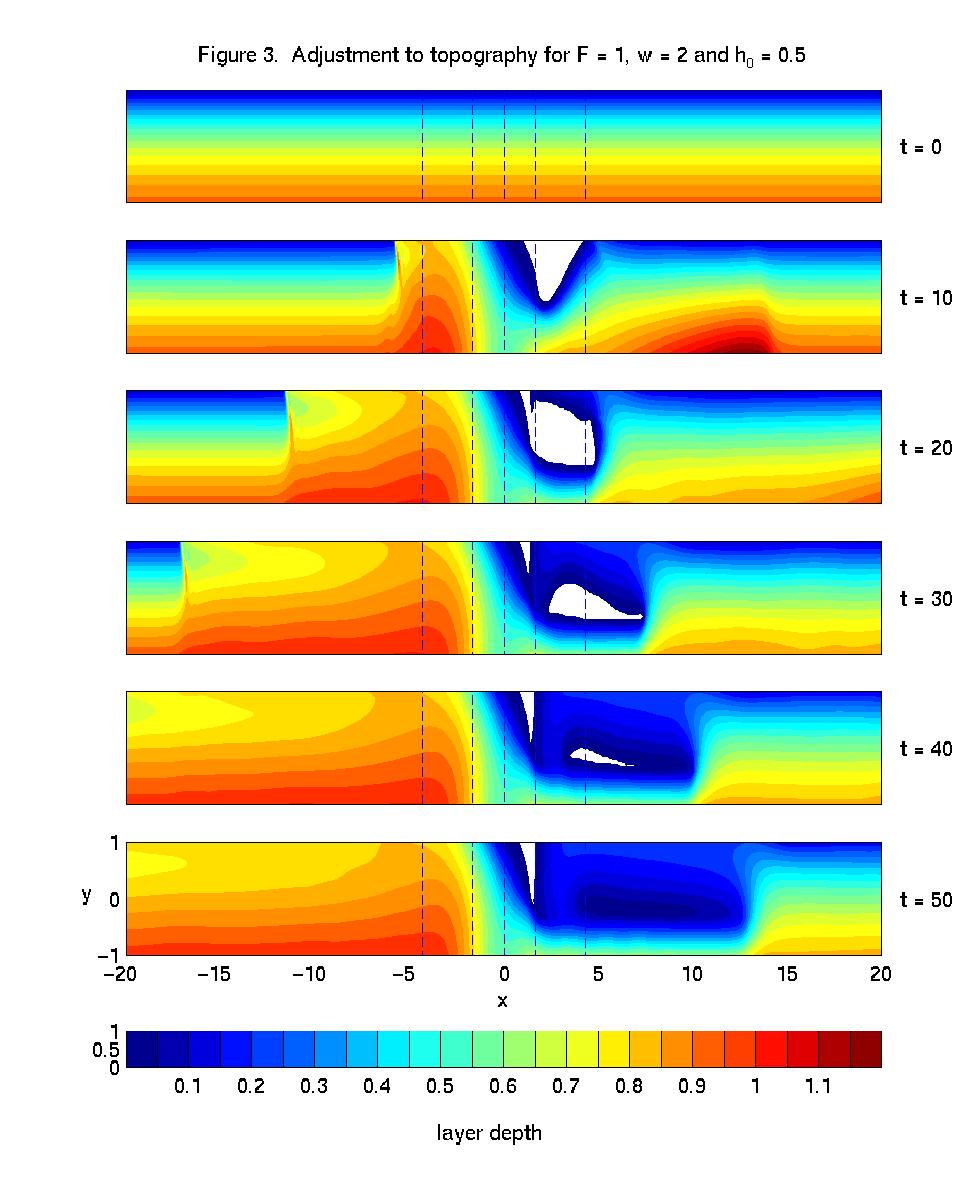Figure 3
The theory is supplemented by numerical solutions of the full shallow
water equations to explore the temporal development of the flow. The numerical
solutions reveal numerous interesting features including upstream propagating
shocks and separated rarefying intrusions, downstream hydraulic jumps (in
both flow depth and width), flow separation and recirculation. Figure 3
shows one typical example for a channel of w = 2 and initial flow
with F = 1. A symmetric topographic feature of height hm
= 0.5 is grown into the flow between t = 0 and 2. A bore propagates
upstream leaving behind a new subcritical upstream state which becomes
supercritical as it flows over the topographic crest (x = 0). Just
downstream of the topographic crest the flow separates from the left wall
to form an expanding recirculation gyre. A small wedge of separated flow
(zone of zero depth) remains over the topography. The numerical solutions
show the semigeostrophic theory to give a generally good prediction of
the critical obstacle height for upstream influence.
4. Summary
One goal of our work is to better understand the adjustment to hydraulically
controlled flows in rotating channels. A consequence of the adjustment
process, either in the Rossby adjustment problem or in the rotating version
of Long's problem, is the generation of shocks, bores and jumps. In the
context of internal solitary waves, the topic of this workshop, we repeat
that wave generation often occurs due to flow interaction with topography
and so any information on the dynamics of that interaction is useful in
the question of solitary wave generation and propagation. Secondly, the
shocks, bores and jumps we calculate are the fully nonlinear, hydrostatic
limits of the (typically) weakly nonlinear solitary wave and undular bore
solutions. As such, they may provide information on the initial, or boundary,
conditions which result in solitary waves in the far field after enough
time has passed for dispersive effects to become important.
References