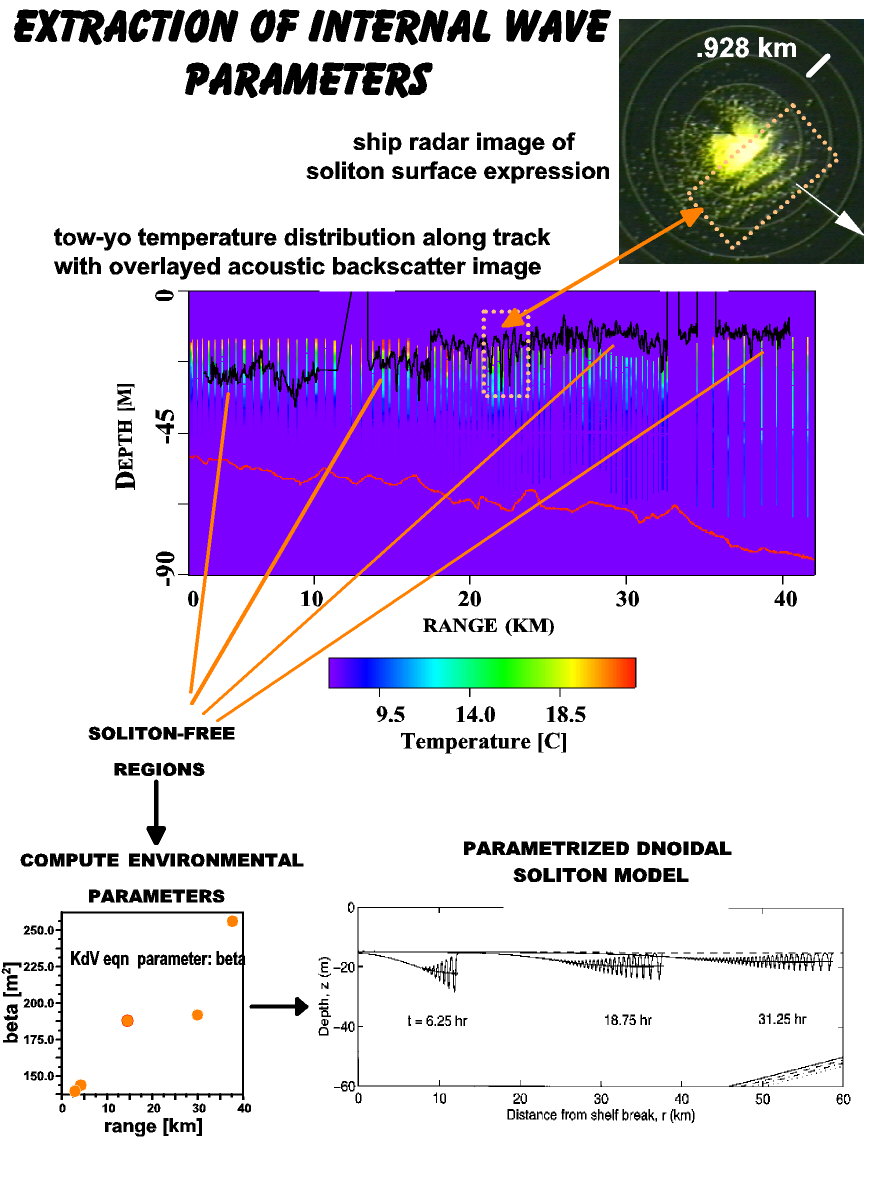
Figure 1
Steven Finette and Marshall Orr
Acoustics Division, Naval Research Lab, Washington DC 20375
John Apel
Global Ocean Associates, P.O. Box 12131, Silver Spring, MD 20908
The SWARM (Shallow Water in a Random Medium) experiment[1] performed on the continental shelf off the New Jersey Coast provided an opportunity to measure acoustic field properties in an area of intense internal wave activity. A number of oceanographic measurements made during the course of the experiment allowed us to develop a model of the internal wavefield, which consisted of both a spatially diffuse component and a spatially localized non-linear contribution from soliton packets. The latter were associated with the leading edge of the M2 internal tide. Both internal wave components evolve in space and time. Below, we briefly consider a model of the soliton packet contribution and illlustrate the time-dependent effect of these soliton components on acoustic field fluctuations as the packets move in a direction anti-parallel to the direction of acoustic propagation.
Tow-yo CTD data were mapped onto the 42 Km acoustic track, and several
points along the track where soliton activity was "low" were determined
from a combination of ship radar images of the surface expression of the
soliton internal wave field and 200 kHz acoustic backscatter measurements
[Fig. 1]. Isolating regions of low soliton activity was necessary because
the mode structure (depth dependence) of the internal wave field depends
only on its linear (spatially diffuse) contribution. These real-time, space
co-incident measurements are illustrated in the figure where the isopycnal
displacements obtained from the acoustic backscatter shown as an overlay
on the tow-yo CTD strips and a radar image is given in the upper right
corner. Buoyancy profiles at these locations were used to compute mode
one internal wave eigenfunctions. The envelope of the isopycnal displacements
describing the time evolution of the soliton packet contribution was obtained
from a solution to the Kortewig-deVries equation, and named the 'dnoidal'
solution [2]. Specification of the solution requires estimates of the coefficients
of the KdV equation (i.e. {a, b} representing the strength of the non-linear
and dispersive terms, respectively), the non-linear phase speed, amplitude
and long wavelength wavenumber. These quantities were estimated by a combination
of data from acoustic backscatter, tow-yo CTD and ship radar measurements
as illustrated in Fig. (1), allowing one to parameterize the soliton model.

Figure 1
A deterministic sound speed distribution estimated from temperature and salinity profiles provided a background environment in which the sound speed variations associated with the packet propagated along the 42 km separation between a vertical line array and a 400 Hz. acoustic source. Bathymetry (shown in the figure as a red curve) and bottom/sediment properties were estimated using a chirp sonar inversion technique[1]. An elastic parabolic equation solver then computed the acoustic field at the array in one minute increments as the environment evolved due to the space-time variations in the soliton packets[3].
An example of the result of this calculation is depicted in Fig. 2,
which shows the time variability of transmission loss and absolute phase
at the array. The time window was approximately 12.4 hours with one minute
increment updates of both soliton and acoustic fields. The upper three
figures in the illustration are snapshots of the sound speed distribution
along the track, showing the superposition of the solitons on the deterministic
background distribution. The red lines connecting these snapshots to the
intensity plot show the approximate times that the snapshots were taken
within an M2 tidal cycle. The sound speed distributions show two packets
traveling to the left (toward the source) in the first two snapshots, with
a space separation between the packets associated with the M2 tide. The
third snapshot contains a single packet, as the one near the array has
now moved off the grid. Sound speed fluctuations associated with these
packets can be as large as 20-30 m/sec. The corresponding transmission
loss at the array as a function of depth and time has a complex structure
that changes qualitatively when packets are no longer near the source and
receiver. The time variations in intensity and phase are associated with
acoustic mode coupling, since the received field under conditions of adiabatic
propagation is not sensitive to the location of the range dependent fluctuations
along the acoustic path. This is strictly true for a range-independent
quiescent environment, since in a range-dependent environment the local
influence of the perturbation can be range dependent. A recent analysis
of mode coupling due to internal waves and its effect on modal intensity
statistics is given in [4]. Temporal phase variations, particularly the
phase gradient along the array, have implications for source localization
schemes such as matched field processing and are under investigation.
Acknowledgement
This research was sponsored by the Office of Naval Research.
References
[1] J.R. Apel,M. Badiey, C.S. Chiu, S. Finette, R. Headrick, J. Kemp, J.R. Lynch, A. Newhall, M.H. Orr, B.H. Pasewark, D. Tielbuerger, K. von der Heydt and S. Wolf: "An Overview of the 1995 SWARM Shallow-Water Internal Wave Acoustic Scattering Experiment", IEEE J. Oceanic Engineering 22 465-500 (1997).
[2] J. Apel, S. Finette, M.O. Orr and J.F. Lynch: "The ?Dnoidal? Model for Internal Solitons and Tides on the Continental Shelf" submitted to J. Geophysical Research (1998).
[3] S. Finette, M.Orr and J.R. Apel: "Acoustic field propagation through a shallow water waveguide dominated by internal waves" Abs. J. Acoust. Soc. Am 102 3062 (1997).
[4] D. Tielbuerger, S. Finette and S. Wolf: "Acoustic propagation through
an internal wave field in a shallow water waveguide" J. Acoust. Soc. Am.
101
789-808 (1997).
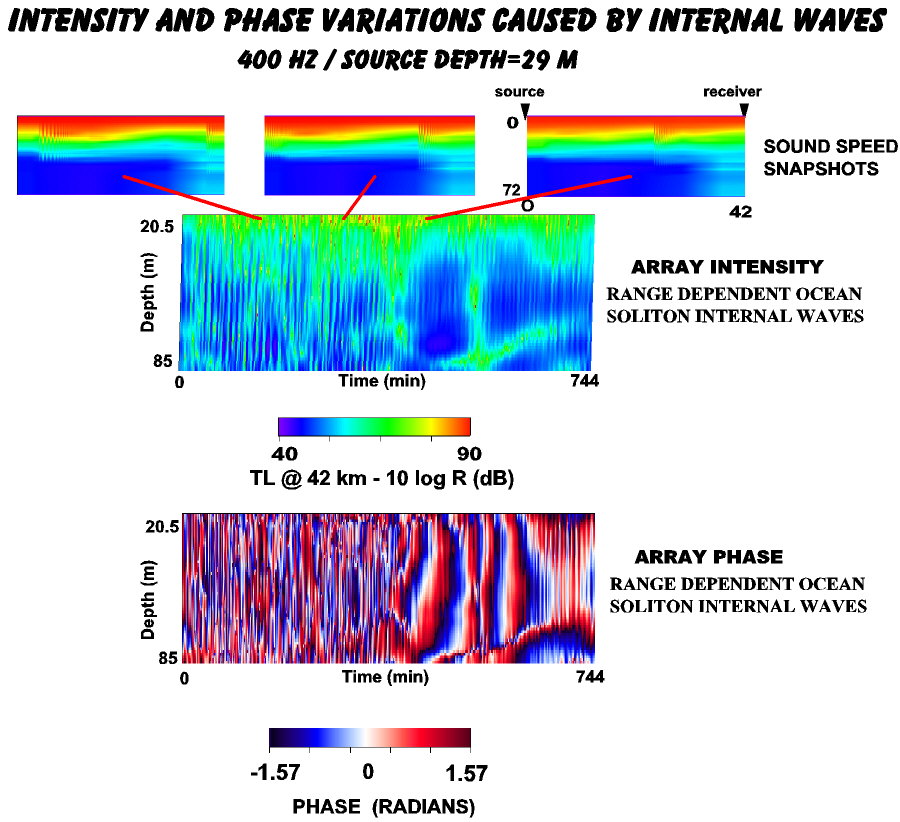
Figure 2