Internal solitary waves are generated as a result of stratified flow over topography. There appear to be several ways in which this can happen, but detailed observations of the generation process are sparse. Here we discuss the generation of waves upstream of the topographic maximum during a strong tidal current and suggest the possible role of shear flow instability in this process. Observations and discussion relating to this presentation appear in Farmer and Armi (1999a).

Calculations of upstream solitary wave generation have been approached in two different ways. Weakly nonlinear models have been used, such as the fKdV or BBM methods. These are suitable for small amplitude features, but their accuracy remains unclear for large amplitude wave generation. Second, the fully nonlinear equations for layered flow have been integrated to simulate upstream solitary wave evolution, following the methods of Roberts and Dold (see abstract by J. Grue in this workshop). However the numerical technique is inherently unstable to small scale instability and filtering is required to remove Kelvin-Helmholtz and related shear flow instabilities.  Even a steady flow over topography can generate upstream solitary wave propagation (i.e. Melville and Helfrich, 1987, Cummins, 1995).  However, the numerical techniques to date have not been suitable for exploring the role of small scale shear flow instability in solitary wave generation.  We present observations of upstream wave generation and suggest two possible routes through which they may be formed.

Our measurements were made by slow ship traverses back and forth across the sill, using a combination of Doppler profiler, acoustic echo-sounder imaging, continuous CTD profiling and a towed vertical string of salinity/temperature/current-meters. Aerial photography was used to map the surface modulations.  All positions were referenced with DGPS. Successive traverses through an increasing tidal current show the internal hydraulic response as the flow gradually becomes established.  As the current slackens, the interface continues to deepen so as to maintain control over the sill crest until relaxation takes place and the current reverses.  The particular process with which we are concerned takes place near maximum tidal current.

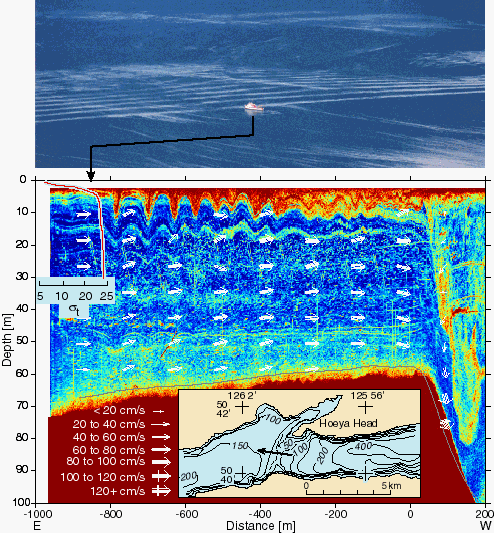
Observations of tidal flow over a sill show trains of internal solitary waves upstream of the crest during periods of strong forcing. The process does not repeat with every tidal cycle and occurs in the subcritical portion of a controlled flow in which the upper layer is drawn down as the current moves over the sill.  Solitary waves appear quite suddenly as the tidal flow develops and may be seen both in aerial photographs and in acoustic measurements (Figure 1).  A characteristic of continuously stratified controlled flows of this kind is the formation of a bifurcation in the streamlines (Farmer and Armi, 1999b).  A quasi-steady internal hydraulic analysis shows that if the bifurcation is forced downstream over the sill crest, it will move very rapidly, even though the tidal current is changing slowly.  Although the quasi-steady approximation can hardly be expected to apply in this case, rapid adjustment is observed.  Moreover, the waves appear at approximately the same time as this adjustment takes place, suggesting that the rapid downstream movement of the bifurcation may itself be responsible for interfacial solitary wave generation.  The waves subsequently advance slowly upstream.

Internal solitary waves also appear to be formed in the presence of shear flow instabilities when there is a more gently sloping interface (Figure 2a,b).  As the ship travels above these instabilities, their instantaneous properties are mapped, analogous to the operation of a focal plane shutter in a camera.  The ship moves faster than the unstable structures, producing in effect a rapid sample of the shear layer in position and time; however some Doppler distortion is unavoidable.   The surface modulation produced by the waves is readily apparent as almost straight slicks formed by the combination of changing color due to thickening of the silt laden surface layer and to the effect of local divergence on the gravity-capillary wave-field.

In a sheared flow, instabilities grow to produce interfacial disturbances that may propagate either with or against the current.  Those travelling downstream are quickly lost and are of little further interest in this context, but those travelling upstream may move faster than the oncoming flow and subsequently evolve into solitary waves.  We distinguish between instabilities created downstream and those formed upstream of the control.  Downstream of the control, all linear waves are swept away, but upstream of the control interfacial waves of sufficient length may escape.

Figure 2c shows the dispersion diagram for internal waves as a function of position, including effects of the variable shear, depth and density structure.  From the perspective of upstream wave generation, instabilities must be of sufficient length to travel against the current.  However, it appears that waves long enough to propagate upstream exceed the length of unstable modes.  We hypothesize that subharmonic interaction could lead to the observed longer wavelengths which also have the required speed. Upstream propagation ducts the waves along a progressively shallower interface so that a wave of small amplitude may eventually become large enough, relative to its distance from the boundary,  to acquire the characteristics of a solitary wave.  The mechanism described here does not necessarily occur in isolation from wave generation caused by time dependent flow over the sill crest.

Since nonlinear waves have higher celerities than linear waves it is possible for them to propagate against the background flow even if they are slightly downstream of the control.  Position B identified in Figure 2c indicates such a location on the dispersion diagram.  Internal solitary waves were observed just downstream of the crest during a flood tide, where they remained trapped for two hours before escaping upstream as the tidal current slackened.   In summary, detailed observations have been acquired of internal solitary waves formed in the vicinity of topography.  In contrast to the nonlinear evolution of internal tides propagating across the continental shelf, the generation mechanism appears closely linked to the internal hydraulic response.

Acknowledgement: This work was supported by the US Office of Naval Research and the Institute of Ocean Sciences.

Additional figures may be viewed at: http://pinger.ios.bc.ca/cruises/knight95/sill.html
 

References:

Farmer, D.  and L. Armi,  The generation and trapping of solitary waves over topography, Science, 283, 188-190, 8 January 1999.

Farmer D. M. and L. Armi,  Stratified flow over topography: the role of small scale entrainment and mixing in flow establishment, in press,
Proc. Roy. Soc., Series A, 1999.

Cummins, P., Numerical simulations of upstream bores and solitons in a two-layer flow past an obstacle, J. Phys. Oceanogr., 25, 1504-1515, 1995.

Melville, W. K. and K. R. Helfrich, Transcritical two-layer flow over topography, J. Fluid. Mech., 178, 31-52, 1987.
 
 

 
Fig. 1 (A) Aerial photograph showing CSS VECTOR about to traverse a group of solitary waves over the sill in Knight Inlet, British Columbia (28 Feb 1995, 0212 UTC). (B) Corresponding echo-sounding image of solitarywaves.  Arrows indicate current vectors shown at same aspect ratio as figure and coded as to magnitude.  Left: Upstream density profile in sigma-t. Inset: Chart of sill area with arrow showing ship track.  Reprinted with permission from Science, Farmer D. and L. Armi, The Generation and Trapping of Solitary Waves over Topography, 8 January 1999, volume 283, pp. 188-190.   Copyright 1999 American Association for the Advancement of Science.
 

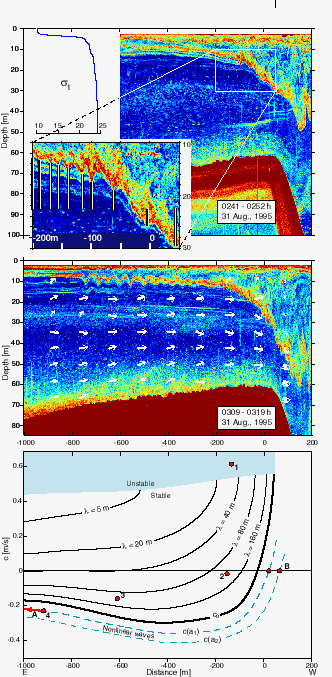
Fig. 2 (A) (Top  Left) Upstream density profile in sigma-t. (Right) Echo-sounding image of downstream traverse showing unstable interface.  (Inset) Vertical lines identify instability scale. (B):  Repeat traverse travelling upstream approximately 30 min after 2a.  (C)  Dispersion diagram for internal waves applicable to A, B propagating against the current.  Dashed curves represent nonlinear waves (not modeled).   Blue shading indicates unstable flow.  '1' '2' represents subharmonic formation of longer waves from instabilities; '2'-'3' represents linear propagation; ('3'-'4') transition to nonlinearity. Reprinted with permission from Science, Farmer D. and L. Armi, The Generation and Trapping of Solitary Waves over Topography, 8 January 1999, volume 283, pp. 188-190.   Copyright 1999 American Association for the Advancement of Science.