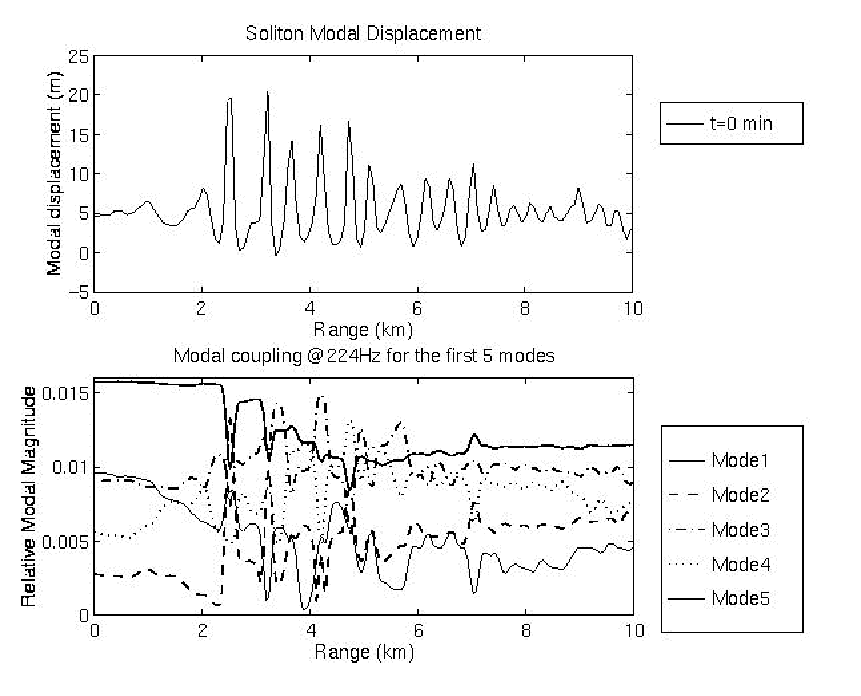
Figure 1. Soliton modal displacement (top) and the relative magnitudes
of the first five acoustic normal modes (bottom).
Figure 2. The 1st baroclinic
internal-wave mode.
Ching-Sang Chiu
Department of Oceanography, Naval Postgraduate School, Monterey, CA 93943
Abstract: Based on moored Acoustic Doppler Current Profiler
(ADCP) data obtained during the 1995 Shallow Water Acoustic Random Media
Experiment (SWARM), the temporal and spatial fluctuations in the sound-speed
field associated with the passage of an internal soliton wavepacket were
synthesized. Using a coupled normal-mode sound propagation model and the
synthesized sound-speed variations, the variability of sound pressure and
of the acoustic modal amplitudes for a 224-Hz CW transmission were simulated.
The auto and cross-correlations of sound pressure at different depths,
and of the acoustic modal amplitudes at a fixed range, were computed for
estimating the vertical and temporal scales of the fluctuating sound field.
The results of the correlation analysis are presented and discussed. [The
research is partially sponsored by the Office of Naval Research.]
Moving forward from the oceanographic findings, the focus of this paper
is on estimating (or predicting) the properties of the fluctuating sound
field. Our method of estimation uses the ADCP observations in conjunction
with an acoustic model. Based on the analyzed ADCP results, the internal
displacement structure of a soliton wavepacket was developed to realistically
synthesize the temporal and spatial fluctuations in the sound-speed field.
Using a coupled normal-mode model for sound propagation and the synthesized
sound-speed variations, the variability of sound pressure and of the acoustic
modal amplitudes along a SWARM acoustic transmission path were simulated.
The auto and cross-correlations of sound pressure at different depths,
and of the acoustic modal amplitudes at fixed ranges, were then computed
for estimating the vertical and temporal scales of the fluctuating sound
field. In this paper, we report the simulated acoustic variability as well
as the results of the correlation analysis for a 224-Hz CW transmission.
The coupled normal-mode model of Chiu et al. [Ref. 2] was employed to
calculate the fluctuating sound field for a 224-Hz CW sound source located
at a depth of 50 m,. At the initial time, i.e., t = 0, the leading edge
of the soliton wavepacket was approximately 2 km from the source. The movement
of the wavepacket was simulated by translating the wavepacket with an observed
phase speed of 0.8333 m/s. "Snap-shots" of the soliton wavepacket were
taken at every 5 seconds to create the sound speed perturbations at those
instances. The sound speed perturbations were simply the products of the
displacements in first baroclinic internal-wave mode and the vertical sound
speed gradients of the mean profile. With such an evolution model of the
sound speeds, the fluctuating acoustic wavefield within a range of 10 km
from the sound source was then calculated at a geophysical time-step of
five seconds over a period of half an hour. This produced time series of
sound pressure at various ranges and depths, as well as time series of
the modal amplitudes at various ranges.

Figure 1. Soliton modal displacement (top) and the relative magnitudes
of the first five acoustic normal modes (bottom).

Figure 2. The 1st baroclinic
internal-wave mode.
To illustrate the significance of mode coupling, the calculated magnitudes
of the first five acoustic modes versus range at t = 0 are displayed in
the bottom panel of Fig. 1. Note that the internal soliton displacements
for the same time is shown on the top. Energy transfer between modes is
evident. For example, Modes 1 and 2 as well as Modes 3 and 5 are easily
seen to be tightly coupled. As energy in one mode increases, the energy
in the other mode decreases. It can also be seen that mode coupling takes
place as soon as the sound energy passes the leading edge of the soliton
wavepacket, particularly in the vicinity of the local peaks in the wavepacket.
Where the internal displacements are small, i.e., at the back of the leading
portion of the wavepacket, the coupling between modes is mild. Active energy
exchange between modes, thus largely occurs within the leading portion
of the wavepacket. Figure 4 shows the variability of the magnitudes of
Mode 1 and Mode 2 over the modeled duration of 30 min. Again, it is seen
that the modal magnitudes change abruptly at the leading edge of the soliton
wavepacket as the wavepacket propagates toward the sound source. The fluctuations
in the modal amplitudes have the same time-scale as the TL, which is about
10 min.
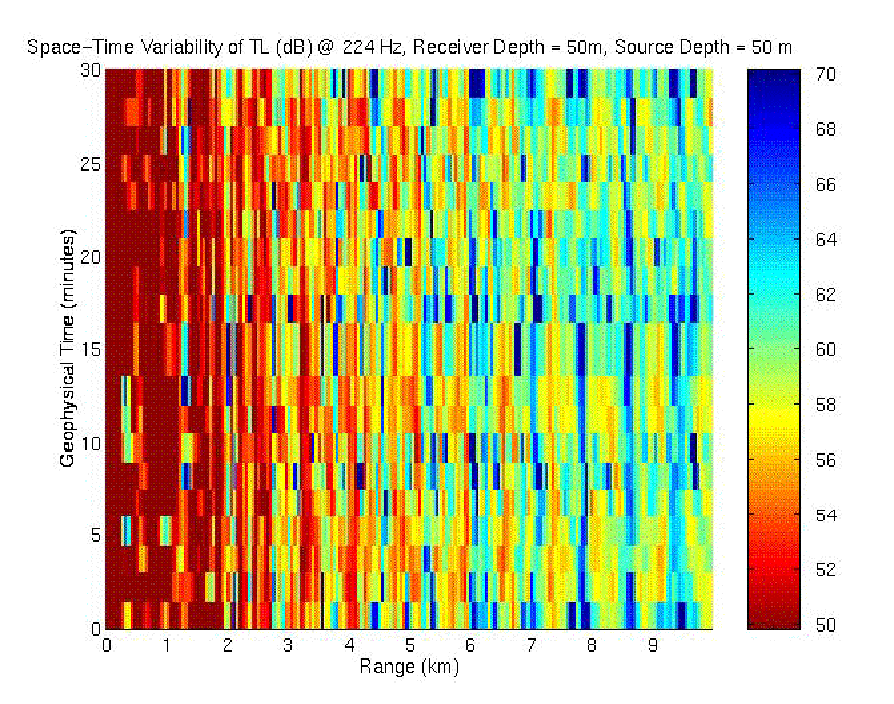
Figure 3. Space-time variability of transmission loss.
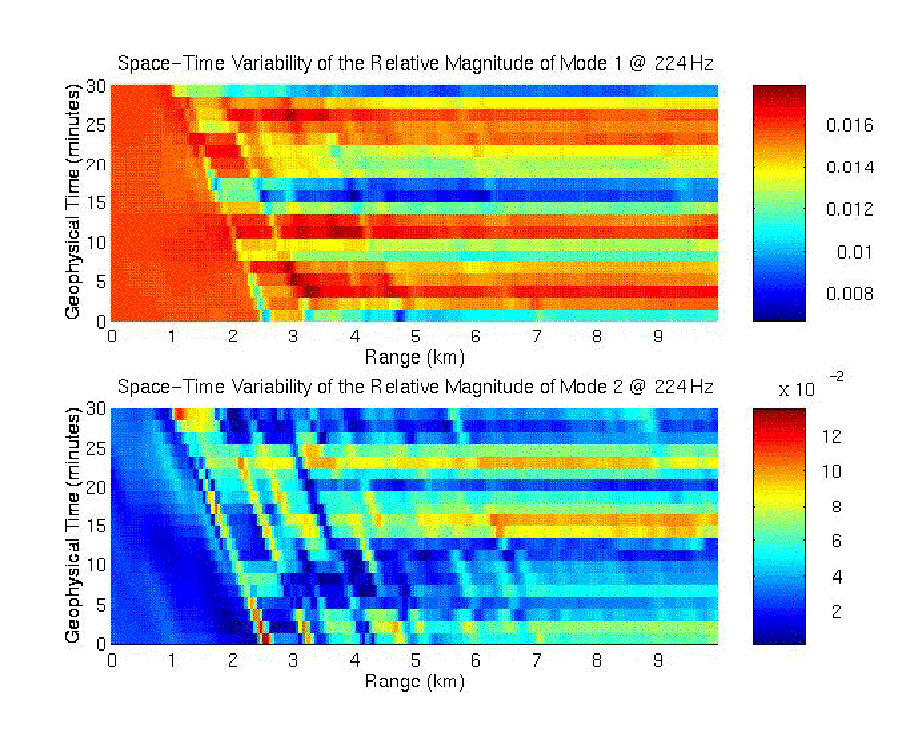
Figure 4. Space-time variability of the relative magnitudes of Mode 1 (top) and Mode 2 (bottom).
To investigate the correlation (vertical) distance and time of the sound pressure field, the receptions by seven hydrophones representing a vertical line array (VLA) located at 10 km from the 224-Hz CW sound source were synthesized. The top phone is located at a depth of 10-m and the bottom phone at 70 m. These hydrophones are labeled as Phone 1 to 7 from top to bottom. The depth spacing between adjacent hydrophones is 10 m. Table 1 shows the auto and cross-correlation coefficients (at zero lag) of the synthesized time records of complex sound pressure perturbation at the seven depths. For all the cross-correlation functions computed, the peaks occur at zero lag. This indicates that the sound field is dominated by the low modes or the low grazing-angle acoustic energy. High correlations of the sound pressure perturbations over the entire VLA (or the entire water depth) are obtained. This outcome is expected because the large-amplitude soliton wavepacket affects a major portion of the shallow water column producing sound speed fluctuations that are in phase at all depths.
Table 2 shows the de-correlation times estimated from the auto-correlation functions of the sound pressure perturbation time series. The de-correlation time is taken to be the lag at which the correlation coefficient drops to a value of 0.3679, i.e., e-1.. A de-correlation time of 50-60 seconds is found at all the hydrophones. The sound pressure perturbations at the various depths along the VLA are likely to have similar structure again due to the shallow water depth and the large-amplitude and vertically in-phase sound-speed changes.
The de-correlation times of the various acoustic modes are tabulated
in Table 3. A value of 0.3679 is again used to determine these modal de-correlation
times. There are considerable variability in the de-correlation times of
the various modes. Mode 1 has the longest de-correlation time. Given a
negative sound speed profile in the SWARM site, the soliton wavepackets
are expected to have a lesser impact on Mode 1, since the span of Mode
1 is well below the depths of maximal sound speed perturbation. Due to
the larger vertical spans of the higher modes, they are likely to be more
affected by the soliton wavepacket. Since the de-correlation times of the
modal amplitudes are longer than the sound pressure observed by a single
phone, the use of VLAs in shallow water can be more advantageous. A shorter
de-correlation time in the single-phone measurements is due to the interference
of the multi-modes.
Table 1: Cross-correlation coefficients of the sound pressure perturbations at the seven depths.
| Phone | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | ||||||
| 2 | 0.9310 | 1 | |||||
| 3 | 0.9061 | 0.8432 | 1 | ||||
| 4 | 0.9296 | 0.8535 | 0.9385 | 1 | |||
| 5 | 0.8934 | 0.8276 | 0.9773 | 0.9558 | 1 | ||
| 6 | 0.7599 | 0.6765 | 0.8229 | 0.8277 | 0.8436 | 1 | |
| 7 | 0.8745 | 0.8387 | 0.9679 | 0.9030 | 0.9730 | 0.7720 | 1 |
Table 2: De-correlation times of the sound pressure perturbations at seven depths.
| Phone | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| De-correlation time (s) | 60 | 60 | 50 | 55 | 50 | 55 | 55 |
Table 3: De-correlation times of theamplitudes of acoustic normal modes.
| Mode | 1 | 2 | 3 | 4 | 5 |
| De-correlation time (s) | 300 | 75 | 112 | 90 | 83 |