Peter G. Baines, David Murray and Thierry Ruchon*
CSIRO Atmospheric Research
Aspendale 3195
Australia
1. Introduction
In this paper we describe the results of an experimental study of wavy disturbances on otherwise steady downslope flows of dense fluid into a homogeneous environment. The waves were generated by causing periodic variations in the supply of dense fluid at the top of the slope. The results are compared with a theoretical model of the Korteweg - de Vries type for non-linear disturbances on such flows.
2. Theoretical Preliminaries
As described below, the onset of a supply of dense fluid at the top of the slope sets up a downslope gravity current, which has an approximately uniform thickness down the slope. The dynamics of this steady flow is governed by a balance between the buoyancy force, and the drag of both the bottom surface and the fluid above, giving a mean state governed by
![]() , (2.1)
, (2.1)
where U is the mean speed of the dense current, d is its thickness, g¢ = gD r /r is the buoyancy, r is the ambient fluid density and D r is the additional density of the dense fluid, CD is the drag coefficient of the bottom and k is an effective drag coefficient for the overlying fluid.
If we consider disturbances propagating on this flow and write
![]() , (2.2)
, (2.2)
one may obtain an equation for h of the form
![]() , (2.3)
, (2.3)
where
![]() , (2.4)
, (2.4)
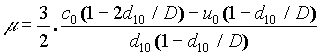 , (2.5)
, (2.5)
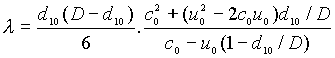 , (2.6)
, (2.6)
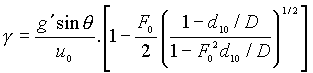 ,
, 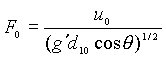 .
(2.7)
.
(2.7)
Here D is a mean total depth, u0 is
the speed of the lower layer, d10 is the depth of the lower
layer and F0 is a Froude number based on the lower layer
alone. The expressions for l and m
are
obtained from Grimshaw (1996). The parameter g
may be positive or negative depending on whether F0 is
greater or less than 2. Some solutions to (2.3) with external forcing have
been given by Smyth (1988). Equation (2.3) itself does not appear to possess
solitary wave solutions, but it presents us with a basis for comparisons
between these dynamics and the experiments.
3. The Experiments
The experiments were carried out in a rectangular glass-sided tank that was approximately 80 cm high, with internal dimensions of 299 cm in length and 38 cm in width, open at the top with a horizontal bottom. The configuration was similar to that described in Baines (1998a,b) for stratified experiments. Only part of the width (23 cm) of the tank was used for the downslope experiments; this was partitioned from the remainder of the tank by a vertical perspex wall that ran along its length, with a gap of 35 cm at one end. At the other end, in this working part, a horizontal shelf 40 cm in length was fitted against the end wall, and this was extended further by a downward slope at 3° to the horizontal, two metres in length. A barrier (or gate) was fitted on the horizontal shelf with a gap of 1 cm at the bottom, at a distance of 40 cm from the end of the tank (i.e. at the top of the slope). In a typical experiment, the tank was filled with fresh water to a depth above the gap at the bottom of this barrier, and a steady flow of dense salty water was supplied by a hose at the end of the tank, to provide a dense downslope-flowing bottom current. Porous mesh barriers were placed 10 cm from the end of the tank to reduce the turbulence generated by the inflow from the hose. The arrangement of these barriers ensured that the flow emerging from them was effectively uniform across the width of the working region. Before each run, a solid temporary barrier was inserted on the shelf. It was then removed at the start of the experiment to ensure a sudden onset to the downslope flow, which was sustained for a typical period of several minutes. At the bottom of the two-metre slope, the dense fluid overflowed the end in a stratified waterfall, accumulating in a pool on the floor of the tank.
The above procedure produced steady currents of dense fluid flowing down the slope. The object of the experiment was to study waves on this current, and to do this a wave generator was inserted on the shelf between the two barriers. Several types of generator were tried, and the design adopted consisted of a mechanically driven movable perspex paddle, spanning the width of the tank and oriented vertically across it. This paddle moved in an elliptical path, forward towards the slope, then upwards, back, down and then forwards again. This had the effect of producing a succession of surges in the current, that took the form of waves of elevation when they emerged onto the top of the slope from under the gate. The amplitude of the stroke of the paddle was 2.7 cm with a period of 3.6 sec for a full circuit of its motion, and this was unchanged for all the experiments described here. The properties of the waves produced were studied for a variety of densities of the inflow and initial flow rates. For virtually all experiments, F0 < 2.
4. Observations and Results
In all experiments, the downslope flow reached a steady state before the motion of the wave-generating paddle was commenced. This downflow was observed to have effectively uniform thickness down the slope, and its dynamical balance is therefore largely governed by (2.1). For the smaller flow rates Q these flows are nearly laminar, but as Q increases they progressively develop features of Kelvin-Helmholtz waves, implying mixing with the fluid above. This tends to cause some degree of downslope flow in this fluid also (Ellison and Turner 1959), which becomes more pronounced as one moves further down the slope, but these effects are relatively small here and will be neglected for the purposes of describing the waves.
The waves generated on these currents had a characteristic life cycle of growth and decay, which is illustrated in Figure 1. Typically, at the top of the slope, the newly generated wave had a smooth, laminar and nearly symmetric appearance. As it moved down the slope with (and faster than) the mean current, it grew in amplitude and steepened on its forward face. This continued until some roughness appeared on the lee side, which then became more pronounced and developed into a full turbulent wake of the wave. This lee-side turbulence had the effect of removing fluid from the rear of the wave and mixing it with the environment, so that shortly after reaching its maximum amplitude and steepness, the wave collapsed as a result of this lee-side turbulent erosion. This left a residual lower, flattener wave structure of decaying turbulent dense fluid. This final process of collapse was often quite sudden and dramatic.
This cycle was not always repeated in exactly the same fashion in all experiments, partly because the variations in the current meant that the initial wave was different and began at different parts of this cycle, with breaking occurring earlier in a more turbulent current than in a laminar one.
For solitary waves with g = 0, from (2.3) their speed is given by
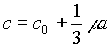 , (4.1)
, (4.1)
where a is the amplitude of the wave. For most
of their life cycle, the observed speeds of the waves were consistent with
this. However, the g -term is generally not
negligible, being often
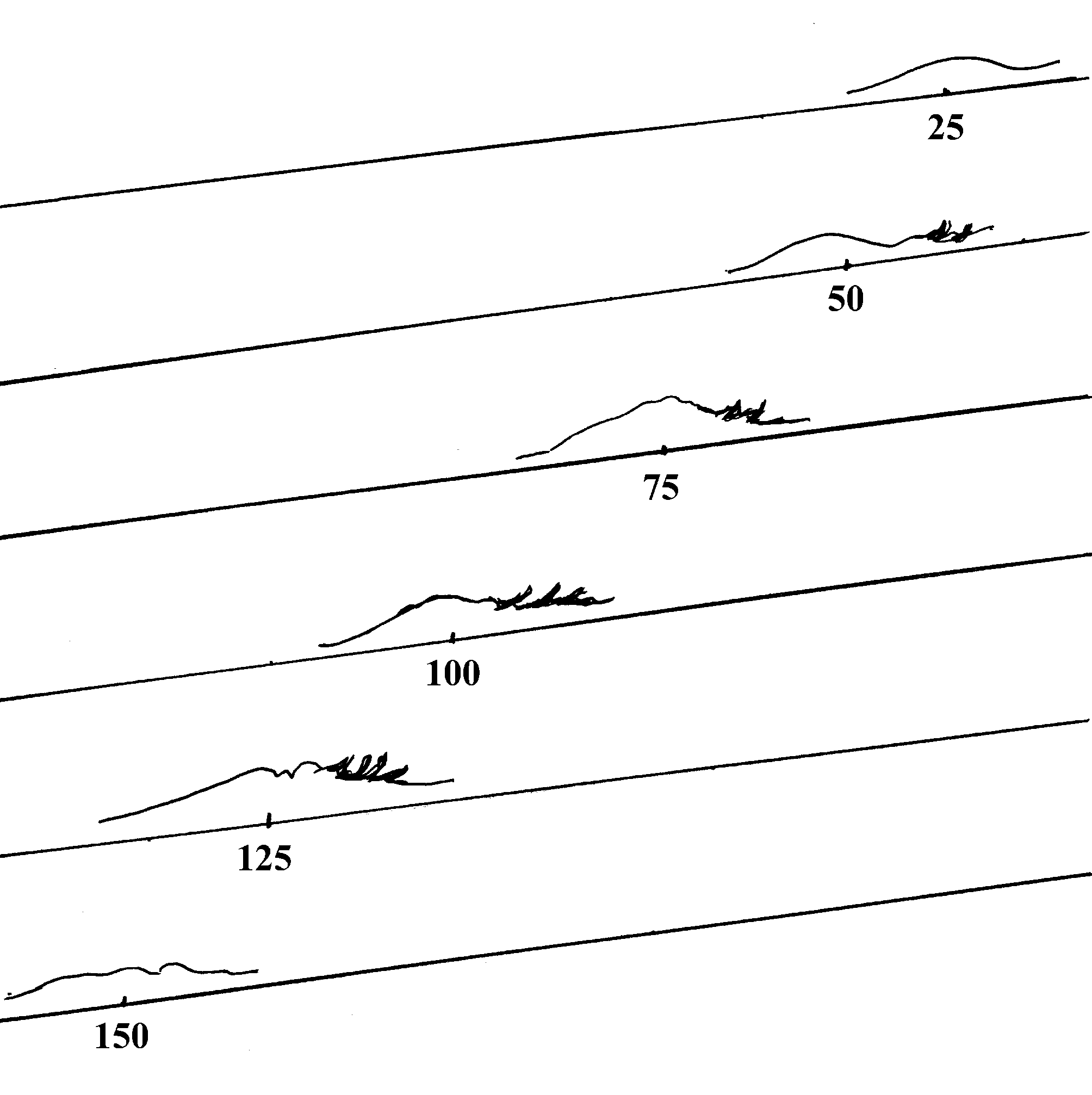
Figure 1. Sketch
of the growth and decay of an isolated wave disturbance as it propagates
down the slope, for F0 = 0.51. The
numbers denote distance from the top of the slope in cm.
larger than the dispersion term (with factor l ). The observed values of other properties relating to (3.2) showed considerable scatter, and this model does not seem to be the most suitable for these waves. This question is being pursued further.
5. Conclusions
The most prominent observed property of the waves was a cycle of growth and decay, which was not satisfactorily described by the model of Section 2. Specifically, the waves grow in amplitude as they move down the slope, and during this phase their speed is generally consistent with (2.3), as non-linear advection and the dispersive term are small. However, as the wave amplitude grows, dissipation and mixing on the lee side increase in magnitude and rapidly erode the wave. The result is a significant mixing event in which the fluid in the wave is mixed with the environmental fluid above, leaving a residual much lower, flatter wave structure on the lower layer. This process seems to be more related to the steepness of the wave and lee-side wake effects rather than shear flow instability, and theoretical models need to take this process into account in order to describe these waves satisfactorily.
References
Baines, P.G. 1998a: Downslope flows into a stratified environment - structure and detrainment. In Mixing and Dispersion in Stably Stratified Flows. Proc. 5th IMA Conference on Stratified Flows, Dundee. P.A. Davies, editor, to appear.
Baines, P.G. 1998b: Downslope flows into stratified environments. To be submitted to J. Fluid Mech..
Ellison, T. and Turner, J.S. 1959: Turbulent entrainment in stratified flows. J. Fluid Mech. 6, 423-448.
Grimshaw, R.H.J. 1996: Internal solitary waves. Monash University Mathematics Deparment Preprint 96/7.
Smyth. N. 1988: Dissipative effects on the resonant flow of a stratified fluid over topography. J. Fluid Mech. 192, 287-312.