 Figure 1 ... Figure 2
Figure 1 ... Figure 2 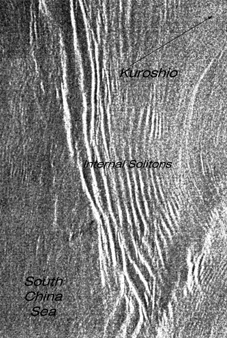
John R. Apel
P.O. Box 12131
Global Ocean Associates
Silver Spring, MD 20908
There are two pervasive, near-global source regions for the generation of internal solitons: (1) continental shelf breaks and (2) undersea sills or ridges protruding into the thermocline. A third, less ubiquitous source is found in the intrusion of fresher, lighter water (such as river outflow or glacial melt water) into the denser water of the sea. The mechanisms that are active in these regions usually involve current flows moving more or less normal to the bathymetry, either onshore or offshore, which have the effect of depressing or elevating the oceanic density distribution away from equilibrium. The excursion, if large enough, will propagate away as an internal solitary wave of some type or other.
One of the uncertainties in the understanding of solitons is found at the next level of detail, e.g.: What are the fluid/bathymetric conditions required for the generation process? For the continental shelf regimes, two hypotheses have been advanced. The first posits that an offshore current flow - typically tidal - forms a lee wave down-current, which may or may not undulate. When the tidal current goes slack, the lee wave, which had been propagating in the moving current at a speed equal and opposite to the current, now continues to hold that speed in the slackening water, and slips up and over the shoal. As it evolves in the radiation region beyond the source area, it oscillates with deepening modulation depth and soon becomes a solitary wave train. The second hypothesis holds that the barotropic ocean tide, when incident upon the continental shelf slope, may scatter into baroclinic modes at the shelf break, thereby setting up the needed density disturbance, which then proceeds as in the first case. For flow over sills, similar mechanisms are at work, but with the space into which it radiates, and thus its ultimate evolution, being different.
With the lee-wave mechanism occurring on the offshore phase of the tide and the baroclinic-scattering mechanism occurring during the onshore phase, they should be readily distinguishable. In fact, it has been difficult to sort them out observationally (R. Chapman, private communication). As Sabinin (K. Sabinin, private communication) has observed, these may be two faces of the same coin, with the different theoretical languages used to discuss them obscuring the possibility that both mechanisms are at work, the first during the offshore flow, followed by the second, during the onshore flow. I would consider the resolution of the generation mechanism questions to be a research priority of high order. These are fully testable hypotheses.
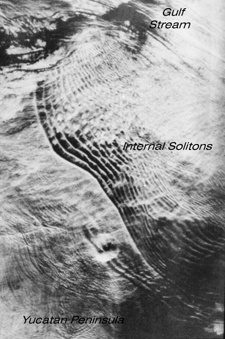
There appears to be yet another kind of region that generates internal
solitons, likely very intense ones. Clear instances of this have been observed
in two satellite images (both SAR). They are (1) the Yucatan Strait, where
the headwaters of the Gulf Stream flow northward between Cuba and Mexico,
and (2) the Luzon Strait between Taiwan and Luzon, where the Kuroshio is
also north-flowing. Figures 1 and 2 show ERS-1 SAR images of these solitons.
Figure 1, of the Yucatan Strait, was provided by D. Sheres, and Fig. 2,
of the South China Sea, by A. K. Liu and M. K. Hsu. The geographical scales
of the two figures are roughly comparable. Both regions are characterized
by strong western boundary current flows that are in the process of turning
from zonal to meridional flow, and by relatively steep topography on the
cyclonic boundary of the current. Both are on the westward sides of the
basins. While the barotropic tide (which is the usual causative agent)
in the Caribbean is not as strong as that in the Western Pacific, and the
geographical tidal exposure of the Yucatan Peninsula is not as great as
the islands in the Luzon Strait, the intensities and dimensions of the
surface signatures are similar.
 Figure 1 ... Figure 2
Figure 1 ... Figure 2 
Most interestingly, both soliton packets are propagating approximately normal to the mean direction of flow. Usually such waves propagate in roughly the same, or essentially opposite to, the direction of the current. Thus these observations raise the questions: Is there some new mechanism operating that produces waves at right angles to the mean flow; or are there simply the familiar processes at work here in unfamiliar geography? Perhaps the ever-present mesoscale meanders of the boundary current systems result in flows with some component normal to the isobaths, so that the old mechanisms can work. This is effective only as the sine of the angle, thereby reducing the component of flow to small values, probably below Froude Number one. Or perhaps the deep, 500-800-m thermocline of the boundary currents provides a buoyancy potential energy storage at the edge of the bathymetric gradient that somehow generates the soliton packet. The question then is where the wave momentum normal to the boundary current flow comes from.
Beyond these intense solitary waves apparently launched from boundary currents near their turning points, there is some scattered evidence that there are analogous but smaller solitons to the north, moving toward the northwest, away from the cyclonic edge of the Gulf Stream. Such have been glimpsed in the Florida current off Cape Canaveral and the Gulf Stream north of Cape Hatteras.
This is a tantalizing problem for which the observational evidence is slim but provocative. It suggests that a modest field program should be undertaken to rough out the situation, perhaps at Yucatan, in order to understand more of what the remotely sensed imagery appears to be telling us.
The theoretical treatment we call the ``dnoidal model''. A paper outlining its properties is currently under review for publication. It asserts that the displacement, (r,z,t) of an isopycnal surface during the passage of an internal soliton can be written as the product of the little-known "dnoidal" solution to the Korteweg-deVries equation for the amplitude, and a numerical solution to the Taylor-Goldstein equation giving the vertical structure function, Wk(z). The KDV solution is one involving the periodic Jacobian elliptic function, dns(r) together with functions that modulate the oscillatory solution, to form three-dimensional wave packets of solitary waves. Under the guidance of field experiments and modeling efforts, it has been generalized to describe the internal tide on the continental shelf as an internal undulatory bore, with a jump discontinuity at the leading edge, soliton oscillations immediately following, and a long-term (tidal period) return to equilibrium at the trailing edge.
An expression for the dnoidal model amplitude is:
Beyond the simple oscillatory dnoidal wave having a vertical
modal (n) structure to it, additional physics included in this relationship
are (1) the modeling of a finite-length wave packet by allowing the nonlinear
parameter s to vary throughout the wave group, (2) an exponential
attenuation factor, and (3) the inclusion of a second, longer-term recovery
function, as represented by the multiplicative quantity, I(r,t),
that converts the expression into one simulating the entire internal tidal
cycle on the continental shelf. A graph of one cycle of this undulatory
``solibore'' is shown in Fig. 3.
Figure 3
The two examples of large solitons presented here are to be included in an Atlas of Internal Solitons currently being produced under ONR sponsorship by myself and associates. The atlas will present some 50 to 60 instances of internal soliton observations at sites around the world, and will include ancillary data on bathymetry, temperature/density profiles, currents, tides, and the like. A theoretical treatment will be used to interpret the data and to provide estimates of wave amplitudes, currents, and phase velocities, which soliton dynamics allows. The atlas will be submitted for publication in about a year but as each example is completed, it will be posted on our web site. We solicit your input to the atlas, with full recognition of any contributions, of course.